题目内容
若三棱锥A—BCD的侧面ABC内一动点P到底面BCD的距离与到棱AB的距离相等,则动点P的轨迹与△ABC组成的图形可能是( )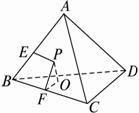
解法一:如图,PO为P到平面BCD的距离,PE为P到棱的距离.过P作PF⊥BC于F,连结OF,则∠PFO为侧面ABC与底面BCD所成二面角的平面角.

设∠PFO=θ,则sinθ=![]() .
.
又PO=PE,
∴sinθ=![]() ,即在侧面ABC内P点到边AB、BC的距离之比为sinθ.故P点的轨迹是直线段.
,即在侧面ABC内P点到边AB、BC的距离之比为sinθ.故P点的轨迹是直线段.
解法二:如下图,在AC上一定存在一点使得到平面BCD的距离和它到AB的距离相等,假设为E点,则EO⊥平面BCD于O,EF⊥AB于F,且EF=EO,连结BE,则BE即为所求.
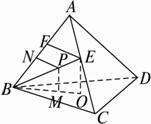
证明:∵EF=EO,BE=BE,
∴Rt△EFB≌Rt△EOB.
∴∠EBF=∠EBO.
设P为BE上任一点,PN⊥AB,PM⊥平面BCD,M、N为垂足,M必在BO上,易证Rt△PNB≌Rt△PMO,
∴PN=PM.
答案:D

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
