题目内容
边长为1的正方形ABCD沿AC对折成二面角B-AC-D，若三棱锥A-BCD的体积是
，则二面角B-AC-D的大小等于
| ||
| 24 |
60°，120°
60°，120°
．分析：如图所示，先作出∠BOD为二面角B-AC-D的平面角．在面BOD内过B作BH⊥OD，则BH⊥面ACD．BH为B到面ACD的距离．利用体积转化V A-BCD=V B-ACD，求出BH，在RT△BOH中求解．
解答：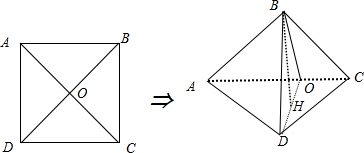
解：如图所示：
在正方形ABCD中连接AC，BD交于点O，
则BO⊥AC，DO⊥AC，∴∠BOD为二面角B-AC-D的平面角，且AC⊥面BOD，
∵AC?面ACD，∴面ACD⊥面BOD．
在面BOD内过B作BH⊥OD，根据平面和平面垂直的性质定理，得BH⊥面ACD．BH为B到面ACD的距离．
∵V A-BCD=V B-ACD=
×
×BH=
，∴BH=
．
在RT△BOH中，sin∠BOD=
=
=
，∠BOD=60°，
若二面角B-AC-D为钝二面角，则大小为180°-60°=120°．
故答案为：60°，120°．
解：如图所示：在正方形ABCD中连接AC，BD交于点O，
则BO⊥AC，DO⊥AC，∴∠BOD为二面角B-AC-D的平面角，且AC⊥面BOD，
∵AC?面ACD，∴面ACD⊥面BOD．
在面BOD内过B作BH⊥OD，根据平面和平面垂直的性质定理，得BH⊥面ACD．BH为B到面ACD的距离．
∵V A-BCD=V B-ACD=
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 24 |
| ||
| 4 |
在RT△BOH中，sin∠BOD=
| BH |
| BO |
| ||||
|
| ||
| 2 |
若二面角B-AC-D为钝二面角，则大小为180°-60°=120°．
故答案为：60°，120°．
点评：本题考查二面角的大小计量，体积的计算即转化，考查空间想象能力，推理论证、运算求解能力．注意结果有两种情况，且大小互补．
练习册系列答案
相关题目
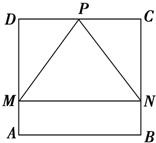如图，四边形ABCD是一个边长为1的正方形，△MPN是正方形的一个内接正三角形，且MN∥AB，若向正方形内部随机投入一个质点，则质点恰好落在△MPN的概率为（ ）
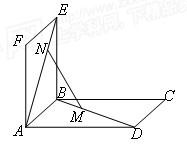如图，两个边长为1的正方形ABCD与ABEF相交于AB，∠EBC=90°，M，N分别是BD，AE上的点，且AN=DM．
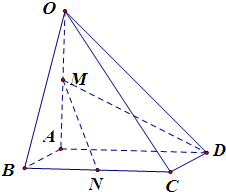如图，在四棱锥O-ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC中点，以A为原点，建立适当的空间直角坐标系，利用空间向量解答以下问题
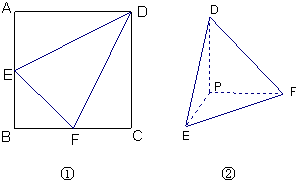（2011•揭阳一模）如图①边长为1的正方形ABCD中，点E、F分别为AB、BC的中点，将△BEF剪去，将△AED、△DCF分别沿DE、DF折起，使A、C两点重合于点P得一三棱锥如图②示．