题目内容
6.已知函数f(x)=$\sqrt{x}$+1,g(x)=alnx,若在x=$\frac{1}{4}$处函数f(x)与g(x)的图象的切线平行,则实数a的值为$\frac{1}{4}$.分析 分别求得函数f(x),g(x)的导数,求得切线的斜率,由两直线平行的条件可得斜率相等,解方程可得a的值.
解答 解:f(x)=$\sqrt{x}$+1,g(x)=alnx的导数分别为$f'(x)=\frac{1}{2}{x^{-\frac{1}{2}}},g'(x)=\frac{a}{x}$,
由在x=$\frac{1}{4}$处函数f(x)与g(x)的图象的切线平行,即为斜率相等,
即有$f'(\frac{1}{4})=g'(\frac{1}{4})$,即$\frac{1}{2}$•$(\frac{1}{4})^{-\frac{1}{2}}$=4a,
则$a=\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查导数的运用:求切线的斜率,考查两直线平行的条件:斜率相等,正确求得导数是解题的关键.

练习册系列答案
相关题目
14.若圆M:(x-3)2+(y-4)2=R2存在两点使其与F1(-2,0),F2(2,0)所张的角为$\frac{π}{2}$,则R的取值范围( )
| A. | 2<R<8 | B. | 2<R<4 | C. | 4<R<9 | D. | 3<R<7 |
11.如图,由曲线y=x2和直线y=$\frac{1}{4}$,x=1,x=0所围成的图形(阴影部分)的面积是( )
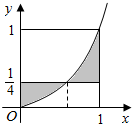

| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
 如图所示,A,B,C是一条公路上的三点,BC=2AB=2km,从这三点分别观测一塔P,从A测得塔在北偏东60°,从B测得塔在正东,从C测得塔在南偏东60°,求该塔到这条公路的距离.
如图所示,A,B,C是一条公路上的三点,BC=2AB=2km,从这三点分别观测一塔P,从A测得塔在北偏东60°,从B测得塔在正东,从C测得塔在南偏东60°,求该塔到这条公路的距离.