题目内容
3．设A、B分别为（1+x）n展开式中的奇数项之和与偶数项之和，则A2-B2的值为（ ）| A． | （1+x）2n | B． | （1-x）n | C． | （1-x2）n | D． | 2n+1 |
分析 由题意可得，（1+x）n =${C}_{n}^{0}$+${C}_{n}^{1}$•x+${C}_{n}^{2}$•x2+${C}_{n}^{3}$•x3+…+${C}_{n}^{n}$•xn=A+B，且（1-x）n =${C}_{n}^{0}$-${C}_{n}^{1}$•x+${C}_{n}^{2}$•x2-${C}_{n}^{3}$•x3+…+（-1）n•${C}_{n}^{n}$•xn=A-B，从而求得A2-B2 的值．
解答 解：由题意可得，（1+x）n =${C}_{n}^{0}$+${C}_{n}^{1}$•x+${C}_{n}^{2}$•x2+${C}_{n}^{3}$•x3+…+${C}_{n}^{n}$•xn=A+B，
（1-x）n =${C}_{n}^{0}$-${C}_{n}^{1}$•x+${C}_{n}^{2}$•x2-${C}_{n}^{3}$•x3+…+（-1）n•${C}_{n}^{n}$•xn=A-B，
∴A2-B2=（1-x2）n，
故选：C．
点评 本题主要考查二项式定理的应用，明白二项式的结构巧妙赋值是解答本题的关键属于基础题．
练习册系列答案
天天练口算系列答案
相关题目
13．如图是一个程序框图，它的功能是（ ）
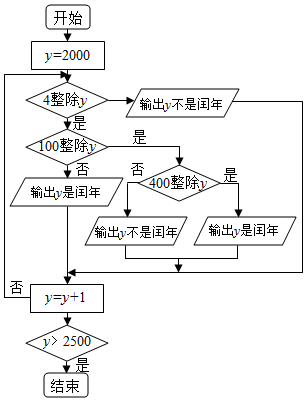
| A． | 输出年份y∈[2000，2500）且y∈N“哪年是闰年”“哪年不是闰年” | |
| B． | 输出年份y∈[2000，2500]且y∈N“哪年是闰年”“哪年不是闰年” | |
| C． | 输出年份y∈[2000，2500）且y∈N“多少年是闰年”“多少年不是闰年” | |
| D． | 输出年份y∈[2000，2500]且y∈N“多少年是闰年”“多少年不是闰年” |