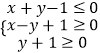题目内容
【题目】我国西部某省4A级风景区内住着一个少数民族村，该村投资了800万元修复和加强民俗文化基础设施，据调查，修复好村民俗文化基础设施后，任何一个月内（每月按30天计算）每天的旅游人数f（x）与第x天近似地满足f（x）=8+ 
（千人），且参观民俗文化村的游客人均消费g（x）近似地满足g（x）=143﹣|x﹣22|（元）．
（1）求该村的第x天的旅游收入p（x）（单位千元，1≤x≤30，x∈N*）的函数关系；
（2）若以最低日收入的20%作为每一天纯收入的计量依据，并以纯收入的5%的税率收回投资成本，试问该村在两年内能否收回全部投资成本？
【答案】
（1）解：依据题意，有p（x）=f （x）g（x）= 
（1≤x≤30，x∈N*）
= 
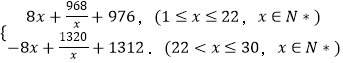
（2）1°当1≤x≤22，x∈N*时，
p（x）=8x+ 
+976≥2 
+976=1152（当且仅当x=11时，等号成立），
因此，p（x）min=p（11）=1152（千元）．
2°当22＜x≤30，x∈N*时，p（x）= 
．
求导可得p′（x）＜0，所以p（x）= 在（22，30]上单调递减，
于是p（x）min=p（30）=1116（千元）．
又1152＞1116，所以日最低收入为1116千元．
该村两年可收回的投资资金为1116×20%×5%×30×12×2=8035.2（千元）=803.52（万元），
因803.52万元＞800万元，所以，该村两年内能收回全部投资资金．
【解析】1、由题意可得 p（x）=f （x）g（x）=
,得到分段函数的解析式。
2、若以最低日收入的20%作为每一天纯收入的计量依据，并以纯收入的5%的税率收回投资成本，选择合适的解析式第一种情况当1≤x≤22，x∈N*时再根据基本不等式求得最小值当且仅当x=11时，等号成立。第二种情况当22＜x≤30，x∈N*时，求导得到p′（x）＜0根据单调性在区间（22，30]上单调递减求得最小值1116千元，又1152＞1116，所以日最低收入为1116千元，再由1116×20%×5%×30×12×2=8035.2（千元）=803.52（万元），根据实际情况该村两年内能收回全部投资资金。
