题目内容
利用证明“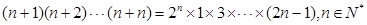 ”时,从假设
”时,从假设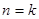 推证
推证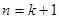 成立时,可以在
成立时,可以在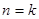 时左边的表达式上再乘一个因式,多乘的这个因式为 ▲ .
时左边的表达式上再乘一个因式,多乘的这个因式为 ▲ .
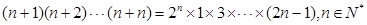 ”时,从假设
”时,从假设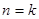 推证
推证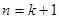 成立时,可以在
成立时,可以在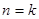 时左边的表达式上再乘一个因式,多乘的这个因式为 ▲ .
时左边的表达式上再乘一个因式,多乘的这个因式为 ▲ . 或
或 (其他化简式不扣分)
(其他化简式不扣分)解:由题意,n="k" 时,左边为(k+1)(k+2)…(k+k);n=k+1时,左边为(k+2)(k+3)…(k+1+k+1);从而增加两项为(2k+1)(2k+2),且减少一项为(k+1),故填写


练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
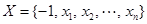 ,其中
,其中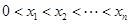 ,
,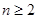 ,定义向量集
,定义向量集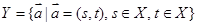 . 若对于任意
. 若对于任意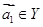 ,存在
,存在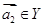 ,使得
,使得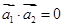 ,则称X具有性质P.例如
,则称X具有性质P.例如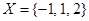 具有性质P.
具有性质P.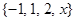 ,求x的值;(4分)
,求x的值;(4分)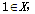 且当xn>1时,x1=1;(6分)
且当xn>1时,x1=1;(6分)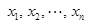 的通
的通 中,
中, 是
是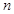 项和,且
项和,且 与
与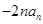 的等差中项,其中
的等差中项,其中 是不等于零的常数.
是不等于零的常数. ; (2)猜想
; (2)猜想 的表达式,并用数学归纳法加以证明.
的表达式,并用数学归纳法加以证明. 中得出的一般性结论是________
中得出的一般性结论是________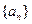 是正数组成的数列,其前n项和
是正数组成的数列,其前n项和 为
为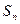 ,对于一切
,对于一切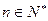 均有
均有 与2的等差中项等于
与2的等差中项等于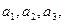 并由此猜想
并由此猜想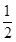 +
+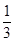 -
-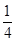 +…+
+…+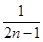 -
-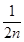 ,则ak+1等于( )
,则ak+1等于( )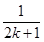
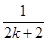 -
-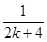
 ”时,在验证
”时,在验证 成立时,左边应该是( )
成立时,左边应该是( )



 时,从“
时,从“ ”变到“
”变到“ ”时,左边应增乘的因式是
”时,左边应增乘的因式是



 中,
中, ,
, ;(Ⅱ)猜想
;(Ⅱ)猜想 的表达式,并用数学归纳法加以证明.
的表达式,并用数学归纳法加以证明.