题目内容
已知 是抛物线
是抛物线 的焦点,
的焦点, 是该抛物线上的动点,则线段
是该抛物线上的动点,则线段 中点的轨迹方程是( )
中点的轨迹方程是( )
A.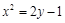 | B. | C. | D. |
A
解析试题分析:抛物线方程可化为: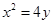 ,焦点
,焦点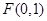 ,设线段
,设线段 中点的坐标为
中点的坐标为 ,
,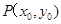 ,所以
,所以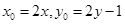 ,代入抛物线方程得:
,代入抛物线方程得: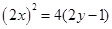 ,即
,即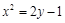 .
.
考点:本小题主要考查用相关点法求轨迹方程.
点评:求轨迹方程时,要注意“求谁设谁”的原则.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
设直线 关于原点对称的直线为
关于原点对称的直线为 ,若
,若 与椭圆
与椭圆 的交点为P、Q, 点M为椭圆上的动点,则使△MPQ的面积为
的交点为P、Q, 点M为椭圆上的动点,则使△MPQ的面积为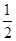 的点M的个数为
的点M的个数为
| A.1 | B.2 | C.3 | D.4 |
设 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线 上一点,
上一点,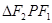 是底角为
是底角为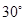 的等腰三角形,则
的等腰三角形,则 的离心率为 ( )
的离心率为 ( )
A. | B. | C. | D. |
已知椭圆的中心在原点,焦点在x轴上,且长轴长为 ,离心率为
,离心率为 ,则椭圆的方程是( )
,则椭圆的方程是( )
A. + + =1 =1 | B. + + =1 =1 | C. + + =1 =1 | D. + + =1 =1 |
已知点 在椭圆
在椭圆 上,则
上,则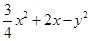 的最大值为( )
的最大值为( )
A. | B.-1 | C.2 | D.7 |
连接抛物线 的焦点
的焦点 与点
与点 所得的线段与抛物线交于点
所得的线段与抛物线交于点 ,设点
,设点 为坐标原点,则三角形
为坐标原点,则三角形 的面积为( )
的面积为( )
A. | B. | C. | D. |
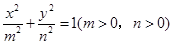 的右焦点与抛物线
的右焦点与抛物线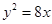 的焦点相同,离心率为
的焦点相同,离心率为 ,则此椭圆的方程为( )
,则此椭圆的方程为( )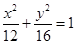

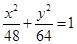
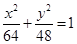
 、
、 ,以
,以 为边作正三角形,若双曲线恰好平分另外两边,则双曲线的离心率为( )
为边作正三角形,若双曲线恰好平分另外两边,则双曲线的离心率为( )



 为抛物线
为抛物线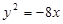 的焦点,
的焦点, 为原点,点
为原点,点 是抛物线准线上一动点,点
是抛物线准线上一动点,点 在抛物线上,且
在抛物线上,且 ,则
,则 的最小值为 ( )
的最小值为 ( )