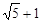题目内容
已知椭圆的中心在原点,焦点在x轴上,且长轴长为 ,离心率为
,离心率为 ,则椭圆的方程是( )
,则椭圆的方程是( )
A. + + =1 =1 | B. + + =1 =1 | C. + + =1 =1 | D. + + =1 =1 |
D
解析试题分析:因为椭圆的中心在原点,焦点在x轴上,所以设椭圆标准方程为: ,因为长轴长为
,因为长轴长为 ,所以
,所以 ,又因为离心率为
,又因为离心率为 ,所以
,所以
 ,所以
,所以 ,所以
,所以 所以椭圆的方程为
所以椭圆的方程为 +
+ =1.
=1.
考点:本小题主要考查了椭圆标准方程的求法,考查学生对椭圆标准方程基本量的理解和掌握.
点评:解题的关键在于掌握椭圆标准方程和基本量并熟练应用,比如长轴长是 ,有的同学会误认为是
,有的同学会误认为是 而导致计算错误.
而导致计算错误.

练习册系列答案
相关题目
椭圆 的一条弦被
的一条弦被 平分,那么这条弦所在的直线方程是 ( )
平分,那么这条弦所在的直线方程是 ( )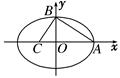
A. | B. |
C. | D. |
已知 为椭圆
为椭圆 的左右焦点,P是椭圆上一点,且P到椭圆左准线的距离为
的左右焦点,P是椭圆上一点,且P到椭圆左准线的距离为
10,若 为线段
为线段 的中点,则
的中点,则 ( )
( )
| A.1 | B.2 | C.3 | D.4 |
若点 和点
和点 分别为椭圆
分别为椭圆 的中心和左焦点,点
的中心和左焦点,点 为椭圆上的任意一点, 则
为椭圆上的任意一点, 则 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
 为抛物线
为抛物线 的焦点,
的焦点, 为抛物线上三点.
为抛物线上三点. 为坐标原点,若
为坐标原点,若 是
是 的重心,
的重心, 的面积分别为
的面积分别为 3,则
3,则 +
+ +
+ 的值为: ( )
的值为: ( )
| A.3 | B.4 | C.6 | D.9 |
 ,则方程
,则方程 表示的曲线不可能是( )
表示的曲线不可能是( )
| A.圆 | B.椭圆 | C.双曲线 | D.抛物线 |
过椭圆 (
( )的左焦点
)的左焦点 作
作 轴的垂线交椭圆于点
轴的垂线交椭圆于点 ,
, 为右焦点,若
为右焦点,若 ,则椭圆的离心率为 ( )
,则椭圆的离心率为 ( )
A. | B. | C. | D. |
 是抛物线
是抛物线 的焦点,
的焦点, 是该抛物线上的动点,则线段
是该抛物线上的动点,则线段 中点的轨迹方程是( )
中点的轨迹方程是( )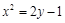



 的左焦点
的左焦点 作圆
作圆 的切线,切点为
的切线,切点为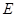 ,延长
,延长 交抛物线
交抛物线 于点
于点 ,若
,若 的中点,则双曲线的离心率为( )
的中点,则双曲线的离心率为( )