题目内容
若(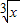 -
-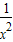 )n的展开式的二项式系数和为128.
)n的展开式的二项式系数和为128.(Ⅰ)求n的值;
(Ⅱ)求展开式中的常数项;
(Ⅲ)求展开式中二项式系数的最大项.
【答案】分析:(Ⅰ)利用(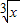 -
-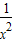 )n的展开式的二项式系数和为128,可得2n=128,从而可求n的值;
)n的展开式的二项式系数和为128,可得2n=128,从而可求n的值;
(Ⅱ)写出展开式的通项,令x的指数为0,即可求展开式中的常数项;
(Ⅲ))(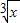 -
-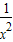 )7的展开式,共8项,第4项与第5项的二项式系数最大,从而可求展开式中二项式系数的最大项.
)7的展开式,共8项,第4项与第5项的二项式系数最大,从而可求展开式中二项式系数的最大项.
解答:解:(Ⅰ)∵(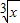 -
-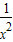 )n的展开式的二项式系数和为128,
)n的展开式的二项式系数和为128,
∴2n=128,∴n=7…(3分)
(Ⅱ)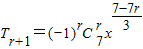 ,令
,令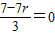 ,r=1,∴常数项为-7…(8分)
,r=1,∴常数项为-7…(8分)
(III)(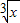 -
-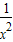 )7的展开式,共8项,第4项与第5项的二项式系数最大
)7的展开式,共8项,第4项与第5项的二项式系数最大
∴最大项为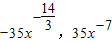 …(12分)
…(12分)
点评:本题考查二项式定理的运用,考查学生的计算能力,正确运用展开式的通项是关键.
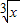 -
-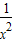 )n的展开式的二项式系数和为128,可得2n=128,从而可求n的值;
)n的展开式的二项式系数和为128,可得2n=128,从而可求n的值;(Ⅱ)写出展开式的通项,令x的指数为0,即可求展开式中的常数项;
(Ⅲ))(
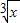 -
-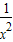 )7的展开式,共8项,第4项与第5项的二项式系数最大,从而可求展开式中二项式系数的最大项.
)7的展开式,共8项,第4项与第5项的二项式系数最大,从而可求展开式中二项式系数的最大项.解答:解:(Ⅰ)∵(
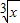 -
-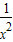 )n的展开式的二项式系数和为128,
)n的展开式的二项式系数和为128,∴2n=128,∴n=7…(3分)
(Ⅱ)
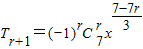 ,令
,令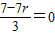 ,r=1,∴常数项为-7…(8分)
,r=1,∴常数项为-7…(8分)(III)(
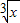 -
-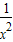 )7的展开式,共8项,第4项与第5项的二项式系数最大
)7的展开式,共8项,第4项与第5项的二项式系数最大∴最大项为
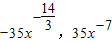 …(12分)
…(12分)点评:本题考查二项式定理的运用,考查学生的计算能力,正确运用展开式的通项是关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
若二项式(
-
)n的展开式的第5项是常数,则自然数n的值为( )
| x |
| 2 |
| x |
| A、6 | B、10 | C、12 | D、15 |
若二项式(
+
)n的展开式的第四项是2
,而第三项的二项式系数是15,则x的取值为( )
| 3 | tan2x |
| 1 |
| tan2x |
| 2 |
| 9 |
A、
| ||
B、kπ-
| ||
C、kπ+
| ||
D、kπ±
|
 )n的展开式的第三项是常数项,则n=________.
)n的展开式的第三项是常数项,则n=________. )n的展开式的第三项是常数项,则n= .
)n的展开式的第三项是常数项,则n= .