题目内容
已知不等式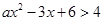 的解集为
的解集为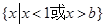 .
.
(1)求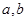 的值;
的值;
(2)解关于 不等式:
不等式: .
.
(1) ;(2)若
;(2)若 ,原不等式的解集为
,原不等式的解集为 ;若
;若 ,原不等式的解集为
,原不等式的解集为 ;
;
若 ,原不等式的解集为
,原不等式的解集为 .
.
解析试题分析:对于(1)可根据根与系数的关系来求解;对于(2),因为方程 可化为
可化为 ,所以根据
,所以根据 和
和 的大小关系来分类讨论不等式的解集.
的大小关系来分类讨论不等式的解集.
试题解析:(1)由题意知方程 的两根为
的两根为 ,
,
从而 解得
解得 ;
;
(2)由条件知 ,即
,即
故若 ,原不等式的解集为
,原不等式的解集为 ;
;
若 ,原不等式的解集为
,原不等式的解集为 ;
;
若 ,原不等式的解集为
,原不等式的解集为 .
.
考点:本题考察了一元二次方程根与系数的关系以及对一元二次不等式的解法,掌握一元二次方程的根与一元二次不等式的解集的关系是解题的关键.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 的不等式
的不等式 的解集为{x∣x<1或x>b}
的解集为{x∣x<1或x>b} 的值
的值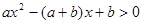
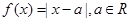
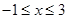 时,
时,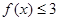 ,求a的取值范围;
,求a的取值范围;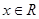 ,
,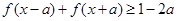 恒成立,求实数a的最小值
恒成立,求实数a的最小值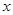 的不等式
的不等式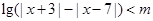 .
.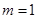 时,解此不等式;
时,解此不等式;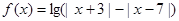 ,当
,当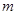 为何值时,
为何值时,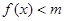 恒成立?
恒成立?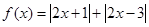 .
. 的不等式
的不等式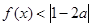 的解集不是空集,求实数
的解集不是空集,求实数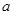 的取值范围;
的取值范围;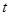 的一元二次方程
的一元二次方程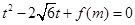 有实根,求实数
有实根,求实数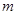 的取值范围.
的取值范围.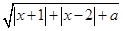 .
. 是定义在
是定义在 上的偶函数,
上的偶函数, ,当
,当 时,
时, .
. ;
;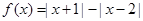 .
.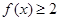 ;
;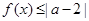 的解集为
的解集为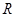 ,求实数
,求实数 的取值范围.
的取值范围.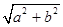 ≥
≥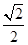 (a+b).
(a+b).