题目内容
3.已知函数f(x)=2x2+2x-b,定义域为(-1,+∞).(Ⅰ)若函数f(x)有1个零点,求实数b的取值范围;
(Ⅱ)若函数f(x)有2个零点,求实数b的取值范围.
分析 (Ⅰ)若函数f(x)有1个零点,转化为f(x)=2x2+2x-b=0,有一个根,利用参数分离法,结合一元二次函数的图象和性质,即可求实数b的取值范围;
(Ⅱ)若函数f(x)有2个零点,转化为f(x)=2x2+2x-b=0,有2个根,结合一元二次函数的图象和性质,即可求实数b的取值范围.
解答 解:(Ⅰ)若函数f(x)有1个零点,
则等价为f(x)=2x2+2x-b=0,有一个根,
即b=2x2+2x在(-1,+∞)上有一个根,
设g(x)=2x2+2x,
作出函数g(x)的图象如图:
则g(x)=2(x+$\frac{1}{2}$)2-$\frac{1}{2}$≥-$\frac{1}{2}$
若b=2x2+2x在(-1,+∞)上有一个根,
则b=-$\frac{1}{2}$或b≥0,
即实数b的取值范围是b=-$\frac{1}{2}$或b≥0.
(Ⅱ)若函数f(x)有2个零点,
则等价为b=2x2+2x在(-1,+∞)上有2个根,
则-$\frac{1}{2}$<b<0.
即实数b的取值范围是-$\frac{1}{2}$<b<0.
点评 本题主要考查函数与方程的应用,利用参数分离法转化为一元二次函数,利用数形结合是解决本题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
8.θ是第二象限角,则下列选项中一定为正值的是( )
| A. | sin$\frac{θ}{2}$ | B. | cos$\frac{θ}{2}$ | C. | tan$\frac{θ}{2}$ | D. | cos2θ |
15.已知全集U=R,集合A={x|x+1<0},B={x|x2+3x<0},则 A∩B等于( )
| A. | {x|-3<x<0} | B. | {x|-3<x<-1} | C. | {x|x<-1} | D. | {x|-1≤x<0} |
13.函数y=xsinx的部分图象是( )
| A. |  | B. | 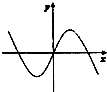 | C. | 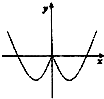 | D. |  |
 已知△ABC的三边长分别为AB=5,BC=4,AC=3,M是AB边上的点,P是平面ABC外一点,给出下列四个命题:
已知△ABC的三边长分别为AB=5,BC=4,AC=3,M是AB边上的点,P是平面ABC外一点,给出下列四个命题: