题目内容
20.给出下列命题:①函数y=cos($\frac{2}{3}x+\frac{π}{2}$)是奇函数;
②若α,β是第一象限角且α<β,则tanα<tanβ;
③x=$\frac{π}{8}$是函数y=sin(2x+$\frac{5π}{4}$)的一条对称轴;
④函数y=sin(2x+$\frac{π}{3}$)的图象关于点($\frac{π}{12},0$)成中心对称.
其中正确命题的序号为( )
| A. | ①③ | B. | ②④ | C. | ①④ | D. | ②③ |
分析 利用诱导公式变形,结合函数的奇偶性判断①;举例说明②错误;分别求解当x=$\frac{π}{8}$、$\frac{π}{12}$的函数值判断③④.
解答 解:①函数y=cos($\frac{2}{3}x+\frac{π}{2}$)=-sin$\frac{2}{3}x$,是奇函数,故命题①正确;
②若α,β是第一象限角且α<β,则tanα<tanβ,错误,如α=60°,β=390°,tan$α=\sqrt{3}$,tan$β=\frac{\sqrt{3}}{3}$;
③当x=$\frac{π}{8}$时,函数y=sin(2×$\frac{π}{8}$+$\frac{5π}{4}$)=-1,故命题③正确;
④当x=$\frac{π}{12}$时,函数y=sin(2×$\frac{π}{12}$+$\frac{π}{3}$)=1,
∴命题函数y=sin(2x+$\frac{π}{3}$)的图象关于点($\frac{π}{12},0$)成中心对称错误.
∴正确的命题是①③.
故选:A.
点评 本题考查命题的真假判断与应用,考查了三角函数的图象和性质,是基础题.

练习册系列答案
相关题目
13.下列函数中,当自变量x变得很大时,随x的增大速度增大得最快的是( )
| A. | y=$\frac{1}{100}$ex | B. | y=100lnx | C. | y=x100 | D. | y=100•2x |
8.“a+b是偶数”是“a、b都是偶数”的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充分条件 | D. | 非充分非必要条件 |
15.已知命题p:存在x∈R,使tanx=$\frac{\sqrt{2}}{2}$,命题q:x2-3x+2<0的解集是{x|1<x<2},下列结论:
①命题“p且q”是真命题;
②命题“p且¬q”是假命题;
③命题“¬p或q”是真命题;
④命题“¬p或¬q”是假命题,
其中正确的是( )
①命题“p且q”是真命题;
②命题“p且¬q”是假命题;
③命题“¬p或q”是真命题;
④命题“¬p或¬q”是假命题,
其中正确的是( )
| A. | ②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
5.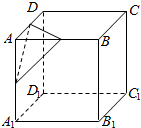 如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )
如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )
 如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )
如图,设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论,其中错误的是( )| A. | 此多面体的表面积为$\frac{47}{8}$a2 | B. | 体对角线AC1垂直于截面 | ||
| C. | 截面平行于平面CB1D1 | D. | 有10个顶点 |
 某高三毕业班甲、乙两名同学在连续的8次数学周练中,统计解答题失分的茎叶图如下:
某高三毕业班甲、乙两名同学在连续的8次数学周练中,统计解答题失分的茎叶图如下: