题目内容
(1)求证:Cn-1m+Cn-1m-2+2Cn-1m-1=Cn+1m;
(2)设(1-
x)2004=a0+a1x+a2x2+…+a2004x2004,其中,a0,a1,a2,…,a2004是常数,求:(a0+a2+a4+…+a2004)2-(a1+a3+a5+…+a2003)2的值.
(2)设(1-
| 2 |
分析:(1)利用组合数的性质:Cnm+Cnm-1=Cn+1m得到Cn-1m+Cn-1m-2+2Cn-1m-1=(Cn-1m+Cn-1m-1)+(Cn-1m-1+Cn-1m-2得证.
(2)将(a0+a2+a4+…+a2004)2-(a1+a3+a5+…+a2003)2的利用平方差公式展开,令(1-
x)2004=a0+a1x+a2x2+…+a2004x2004的x分别取1,-1,代入上式,求出待求的值.
(2)将(a0+a2+a4+…+a2004)2-(a1+a3+a5+…+a2003)2的利用平方差公式展开,令(1-
| 2 |
解答:解:(1)证明:Cn-1m+Cn-1m-2+2Cn-1m-1=(Cn-1m+Cn-1m-1)+(Cn-1m-1+Cn-1m-2)=Cnm+Cnm-1=Cn+1m
所以Cn-1m+Cn-1m-2+2Cn-1m-1=Cn+1m;
(2)令x=1,则有(1-
)2004=a0+a1+a2+…+a2004,
令x=-1则有(1+
)2004=a0-a 1+a2-a3+…+(-1)2004a2004,
所以:(a0+a2+a4+…+a2004)2-(a1+a3+a5+…+a2003)2=1.
所以Cn-1m+Cn-1m-2+2Cn-1m-1=Cn+1m;
(2)令x=1,则有(1-
| 2 |
令x=-1则有(1+
| 2 |
|
|
|
所以:(a0+a2+a4+…+a2004)2-(a1+a3+a5+…+a2003)2=1.
点评:本题考查组合数的性质:Cnm+Cnm-1=Cn+1m,考查利用赋值法求二项展开式的系数和问题,是高考常考题型.

练习册系列答案
相关题目
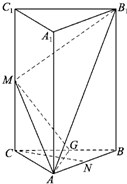 (2012•赣州模拟)如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点.且
(2012•赣州模拟)如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点.且