题目内容
过抛物线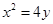 的焦点作直线l交抛物线于A,B两点,分别过A,B作抛物线的切线
的焦点作直线l交抛物线于A,B两点,分别过A,B作抛物线的切线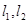 ,则
,则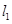 与
与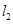 的交点P的轨迹方程是( )
的交点P的轨迹方程是( )
A.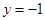 | B.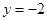 | C.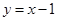 | D.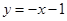 |
A
解析试题分析:抛物线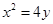 的焦点为
的焦点为 ,设直线
,设直线 的方程为
的方程为 ,代入抛物线方程得
,代入抛物线方程得 ,由根与系数的关系得
,由根与系数的关系得 .设
.设 .由
.由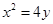 得
得 ,求导得
,求导得 ,则过A,B的抛物线的切线方程分别为
,则过A,B的抛物线的切线方程分别为 ,
, ,即
,即 ,
, .从这两个方程可看出,
.从这两个方程可看出, 是方程
是方程 的两个根,所以
的两个根,所以 .由
.由 及
及 得
得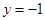 ,即
,即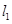 与
与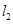 的交点P的轨迹方程是
的交点P的轨迹方程是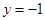 .
.
考点:轨迹与方程.

练习册系列答案
相关题目
抛物线 的焦点到准线的距离是( )
的焦点到准线的距离是( )
| A.2 | B.1 | C. | D. |
已知直线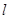 与双曲线
与双曲线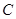 交于
交于 ,
, 两点(
两点( ,
, 在同一支上),
在同一支上),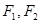 为双曲线的两个焦点,则
为双曲线的两个焦点,则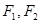 在( )
在( )
A.以 , , 为焦点的椭圆上或线段 为焦点的椭圆上或线段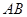 的垂直平分线上 的垂直平分线上 |
B.以 , , 为焦点的双曲线上或线段 为焦点的双曲线上或线段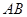 的垂直平分线上 的垂直平分线上 |
C.以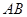 为直径的圆上或线段 为直径的圆上或线段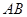 的垂直平分线上 的垂直平分线上 |
| D.以上说法均不正确 |
设椭圆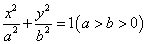 的离心率
的离心率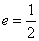 ,右焦点
,右焦点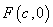 ,方程
,方程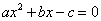 的两个根分别为
的两个根分别为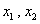 ,则点
,则点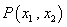 在( )
在( )
A.圆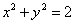 上 上 |
B.圆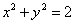 内 内 |
C.圆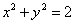 外 外 |
| D.以上三种都有可能 |
抛物线 的焦点坐标为( )
的焦点坐标为( )
A. | B. | C. | D. |
 的焦点F与椭圆
的焦点F与椭圆 的左焦点重合,点A在抛物线上,且
的左焦点重合,点A在抛物线上,且 ,若P是抛物线准线上一动点,则
,若P是抛物线准线上一动点,则 的最小值为( )
的最小值为( )


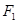 、
、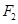 分别是椭圆
分别是椭圆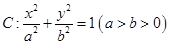 的左、右焦点,点
的左、右焦点,点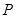 在椭圆
在椭圆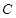 上,线段
上,线段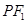 的中点在
的中点在 轴上,若
轴上,若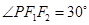 ,则椭圆的离心率为( )
,则椭圆的离心率为( )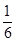
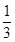
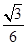
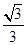
 的焦点为
的焦点为 ,点
,点 在抛物线上,且
在抛物线上,且 ,弦
,弦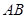 中点
中点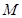 在准线
在准线 上的射影为
上的射影为 的最大值为( )
的最大值为( )




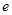 的双曲线和离心率为
的双曲线和离心率为 的椭圆有相同的焦点
的椭圆有相同的焦点 、
、 ,
, 是两曲线的一个公共点,若
是两曲线的一个公共点,若 ,则
,则


