题目内容
(21)已知定义域为R的函数f(x)=(Ⅰ)求a,b的值;
(Ⅱ)若对任意t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.
(Ⅰ)因为f(x)是奇函数,所以f(0)=0,即![]() 解得b=1.
解得b=1.
从而有f(x)=![]()
又由f(1)=-f(-1)知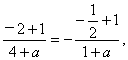 解得a=2.
解得a=2.
(Ⅱ)解法一:
由(Ⅰ)知f(x)=![]()
由上式易知f(x)在(-∞,+∞)上为减函数.
又因f(x)是奇函数,从而不等式f(t2-2t)+f(2t2-k)<0等价于
f(t2-2t)<-f(2t2-k)=f(-2x2+k).
因f(x)是减函数,由上式推得
t2-2t>-2t2+k.
即对一切t∈R有
3t2-2t-k>0.
从而判别式Δ=4+12k<0,解得k<-![]() .
.
解法二:
由(Ⅰ)知f(x)=![]() 又由题设条件得
又由题设条件得
![]()
即![]()
整理得![]() >1,因底数2>1,故
>1,因底数2>1,故
3t2-2t-k>0.
上式对一切t∈R均成立,从而判别式Δ=4+12k<0,解得k<-![]()

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
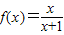 .
.