题目内容
已知定义域为R的函数f(x)是偶函数,当x≥0时,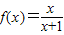 .
.(1)求f(x)的解析式;
(2)证明方程f(x)=21-x在区间(1,2)上有解.
【答案】分析:(1)当x<0时,则-x>0,故 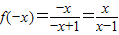 ,由 f(x)是偶函数,可得
,由 f(x)是偶函数,可得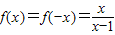 ,
,
从而得到函数的解析式.
(2)令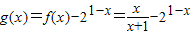 ,x∈(1,2),得到 g(1)•g(2)<0,故方程f(x)=21-x在区间(1,2)上有解.
,x∈(1,2),得到 g(1)•g(2)<0,故方程f(x)=21-x在区间(1,2)上有解.
解答:解:(1)当x<0时,则-x>0,∴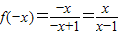 ,∵f(x)是偶函数,
,∵f(x)是偶函数,
∴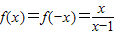 ,∴
,∴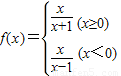 .
.
(2)令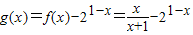 ,x∈(1,2).
,x∈(1,2).
∵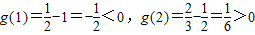 ,∴g(1)•g(2)<0,
,∴g(1)•g(2)<0,
∴方程f(x)=21-x在区间(1,2)上有解.
点评:本题考查偶函数的定义,求函数的解析式,函数的零点与方程的根,令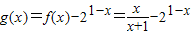 ,x∈(1,2),得到 g(1)•g(2)<0,是解题的关键.
,x∈(1,2),得到 g(1)•g(2)<0,是解题的关键.
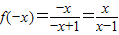 ,由 f(x)是偶函数,可得
,由 f(x)是偶函数,可得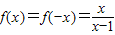 ,
,从而得到函数的解析式.
(2)令
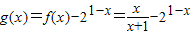 ,x∈(1,2),得到 g(1)•g(2)<0,故方程f(x)=21-x在区间(1,2)上有解.
,x∈(1,2),得到 g(1)•g(2)<0,故方程f(x)=21-x在区间(1,2)上有解.解答:解:(1)当x<0时,则-x>0,∴
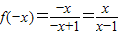 ,∵f(x)是偶函数,
,∵f(x)是偶函数,∴
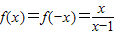 ,∴
,∴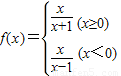 .
.(2)令
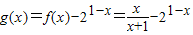 ,x∈(1,2).
,x∈(1,2).∵
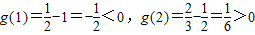 ,∴g(1)•g(2)<0,
,∴g(1)•g(2)<0,∴方程f(x)=21-x在区间(1,2)上有解.
点评:本题考查偶函数的定义,求函数的解析式,函数的零点与方程的根,令
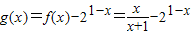 ,x∈(1,2),得到 g(1)•g(2)<0,是解题的关键.
,x∈(1,2),得到 g(1)•g(2)<0,是解题的关键. 
练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目