题目内容

4．命题甲x+y≠8；命题乙：x≠2或y≠6，则（　　）
A．甲是乙的充分非必要条件
B．甲是乙的必要非充分条件
C．甲是乙的充要条件
D．甲既不是乙的充分条件，也不是乙的必要条件．

分析 根据充分条件和必要条件的定义以及逆否命题的等价性即可得到结论．

解答 解：￢甲：x+y=8，￢乙：x=2且y=6，
当x=2且y=6时，x+y=8成立，
当x=1且y=7时满足x+y=8，但x=2且y=6不成立，
即￢乙是￢甲的充分不必要条件，
则根据逆否命题的等价性可知命题甲是命题乙的充分不必要条件，
故选：A．

点评 本题主要考查充分条件和必要条件的判断，根据逆否命题的等价性进行转化是解决本题的关键．否则不太容易判断．

练习册系列答案
相关题目
14．已知数列{an}中，a1=-1，an+1=3an-1，则其通项an=$-\frac{{{3^n}-1}}{2}$．
15．已知函数f（x）=sin2x+sinx+cosx，以下说法中不正确的是（　　）
A．f（x）周期为2πB．f（x）最小值为-$\frac{5}{4}$
C．f（x）在区间[0，$\frac{π}{2}$]单调递增D．f（x）关于点x=$\frac{π}{4}$对称
12．已知函数$f（x）=\frac{e^x}{{a{x^2}+bx+1}}$，其中a，b，c∈R．
（Ⅰ）若a=b=1，求函数f（x）的单调区间；
（Ⅱ）若a=0，且当x≥0时，f（x）≥1总成立，求实数b的取值范围；
（Ⅲ）若a＞0，b=0，若f（x）存在两个极值点x1，x2，求证；f（x1）+f（x2）＜e．
19．已知函数$f（x）=\frac{e^x}{{a{x^2}+bx+1}}$，其中a，b，c∈R．
（Ⅰ）若a=b=1，求函数f（x）的单调区间；
（Ⅱ）若a=0，且当x≥1时，f（x）≥1总成立，求实数b的取值范围．
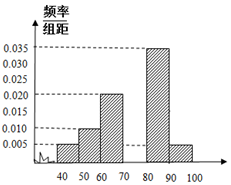9．为了估计某校的一次数学考试情况，现从该校参加考试的600名学生中随机抽出60名学生，其成绩（百分制）均在[40，100）上，将这些成绩分成六段[40，50），[50，60）…[90，100），后得到如图所示部分频率分布直方图．
（1）求抽出的60名学生中分数在[70，80）内的人数；
（2）若规定成绩不小于85分为优秀，则根据频率分布直方图，估计该校优秀人数．
（3）根据频率分布直方图算出样本数据的中位数．
16．某高中计划从全校学生中按年级采用分层抽样方法抽取20名学生进行心理测试，其中高三有学生900人，已知高一与高二共抽取了14人，则全校学生的人数为3000．
13．已知过抛物线y2=2px（p＞0）的焦点，斜率为$2\sqrt{2}$的直线交抛物线于A（x1，y1），B（x2，y2）（x1＜x2）两点，且$|AB|=\frac{9}{2}$．
（1）求该抛物线的方程；
（2）过抛物线上的一个点M（1，2）作两条垂直的直线MP，MQ分别交抛物线于P，Q两点，试问：直线PQ是否过定点，如果过，请求出来，不过，请说明理由．
（3）求原点O到直线PQ的最大距离为多少？
14．对于任意两个正实数a，b，定义a*b=λ×$\frac{a}{b}$．其中常数λ∈（$\frac{\sqrt{2}}{2}$，1），“×”是通常的实数乘法运算，若a≥b＞0，a*b与b*a都是集合{x|x=$\frac{n}{2}$，n∈Z}中的元素，则a*b=$\frac{3}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网