题目内容
9.已知函数f(x)=Asin(x+φ)(A>0,0<φ<π,x∈R)的最大值是1,其图象经过点$M({\frac{π}{3}\;,\;\;\frac{1}{2}})$.(1)求f(x)的解析式;
(2)已知$α\;,\;\;β∈({0\;,\;\;\frac{π}{2}})$,且$f(α)=\frac{3}{5}$,$f(β)=\frac{12}{13}$.求f(α+β)的值.
分析 (1)由题意求出A,将点M的坐标代入化简后,由φ的范围和特殊角的三角函数值求出φ的值,由诱导公式化简后得函数f(x)的解析式;
(2)由(1)和题意求出cosα和cosβ,由α、β的范围和平方关系求出sinα、sinβ,利用两角和的余弦公式求出cos(α+β),可得f(α+β)的值.
解答 解:(1)由题意得,A=1,
∵函数f(x)的图象经过点$M({\frac{π}{3}\;,\;\;\frac{1}{2}})$,
∴$sin(\frac{π}{3}+φ)=\frac{1}{2}$,
由0<φ<π得,$\frac{π}{3}<\frac{π}{3}+φ<\frac{4π}{3}$,
∴$\frac{π}{3}+φ=\frac{5π}{6}$,解得φ=$\frac{π}{2}$,
∴f(x)=sin(x+$\frac{π}{2}$)=cosx;
(2)由题意知,$f(α)=\frac{3}{5}$,$f(β)=\frac{12}{13}$,
由(1)得,cosα=$\frac{3}{5}$,cosβ=$\frac{12}{13}$,
∵$α,β∈(0,\frac{π}{2})$,
∴$sinα=\sqrt{1-co{s}^{2}α}$=$\frac{4}{5}$,同理可得sinβ=$\frac{5}{13}$,
∴cos(α+β)=cosαcosβ-sinαsinβ
=$\frac{3}{5}×\frac{12}{13}-\frac{4}{5}×\frac{5}{13}$=$\frac{16}{65}$,
即f(α+β)的值是$\frac{16}{65}$.
点评 本题考查了形如f(x)=Asin(ωx+φ)的解析式的确定,两角和的余弦公式、平方关系和诱导公式的应用,注意角的范围,考查化简、计算能力.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案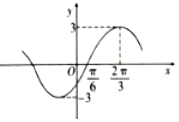
| A. | $y=3sin({2x-\frac{π}{6}})$ | B. | $y=3sin({2x-\frac{π}{3}})$ | C. | $y=3sin({x-\frac{π}{6}})$ | D. | $y=3sin({x-\frac{π}{3}})$ |
| A. | [4,6] | B. | [5,6] | C. | [25,36] | D. | [16,36] |