题目内容
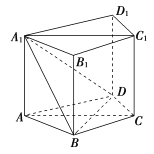
【题目】如图,在以![]() 为顶点的五面体中,底面
为顶点的五面体中,底面![]() 是矩形,
是矩形, ![]() .
.
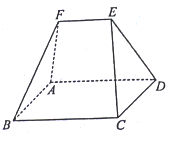
(1)证明: ![]() 平面
平面![]() ;
;
(2)在中国古代数学经典著作《九章算术》中,称图中所示的五面体![]() 为“刍甍”(chúméng),书中将刍甍
为“刍甍”(chúméng),书中将刍甍![]() 的体积求法表述为:
的体积求法表述为:
术曰:倍下袤,上袤从之,以广乘之,又以高乘之,六而一.其意思是:若刍甍![]() 的“下袤”
的“下袤” ![]() 的长为
的长为![]() ,“上袤”
,“上袤” ![]() 的长为
的长为![]() ,“广”
,“广” ![]() 的长为
的长为![]() ,“高”即“点
,“高”即“点![]() 到平面
到平面![]() 的距离”为
的距离”为![]() ,则刍甍
,则刍甍![]() 的体积
的体积![]() 的计算公式为:
的计算公式为: ![]() ,证明该体积公式.
,证明该体积公式.
【答案】(1)见解析;(2)见解析.
【解析】分析:(1)先证明![]() ,再证明
,再证明![]() 平面
平面![]() .(2)利用割补法证明
.(2)利用割补法证明![]()
![]() .
.
详解:(1)证明:![]() 是矩形,
是矩形,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]()
![]()
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.

(2)解:设![]() 分别是棱
分别是棱![]() 上的点,且满足
上的点,且满足![]() ,
,
链接![]() .由第(1)问的证明知,
.由第(1)问的证明知,![]() ,
,
所以四边形![]() 和
和![]() 为平行四边形.
为平行四边形.
![]() ,
,
又![]() ,
,![]() 平面
平面![]() ,
,
![]() 多面体
多面体![]() 为三棱柱.
为三棱柱.
因此,刍甍![]() 可别分割成四棱锥
可别分割成四棱锥![]() 和三棱柱
和三棱柱![]() .
.
由题意知,矩形![]() 中,
中,
![]()
![]()
![]() 矩形
矩形![]() 的面积
的面积![]() ,
,
又四棱锥![]() 的高,即“点
的高,即“点![]() 到平面
到平面![]() 的距离”为
的距离”为![]() ,
,
![]() 四棱锥
四棱锥![]() 的体积
的体积![]() ;
;
三棱柱![]() 的体积可以看成是以矩形
的体积可以看成是以矩形![]() 为底,以点
为底,以点![]() 到平面
到平面![]() 的距离
的距离![]() 为高的四棱柱体积的一半.
为高的四棱柱体积的一半.
又矩形![]() 的面积
的面积![]()
![]() 三棱柱
三棱柱![]() 的体积
的体积![]()
刍甍![]() 的体积:
的体积:
![]()
![]()
![]() .
.
![]() 刍甍
刍甍![]() 体积公式得证.
体积公式得证.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):
| 2 | 3 | 4 | 5 | 6 | 8 | 9 | 11 |
| 1 | 2 | 3 | 3 | 4 | 5 | 6 | 8 |
(Ⅰ)根据上表数据在下列网格中绘制散点图;
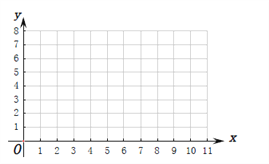
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)在该商品进货量![]() (吨)不超过6(吨)的前提下任取两个值,求该商品进货量
(吨)不超过6(吨)的前提下任取两个值,求该商品进货量![]() (吨)恰有一个值不超过3(吨)的概率.
(吨)恰有一个值不超过3(吨)的概率.
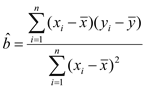 ,
,