题目内容
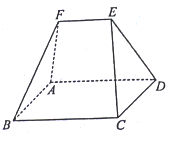
【题目】如图,在直四棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() .
.
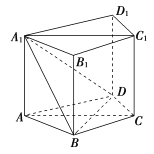
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 时,直线
时,直线![]() 与平面
与平面![]() 所成的角能否为
所成的角能否为![]() ?并说明理由.
?并说明理由.
【答案】(1)证明见解析;(2)答案见解析.
【解析】
(1)由题意结合几何关系可证得![]() ,
,![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)设![]() ,以
,以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() ,不妨设
,不妨设![]() ,
,![]() ,据此可得平面
,据此可得平面![]() 的法向量为
的法向量为![]() ,若满足题意,则
,若满足题意,则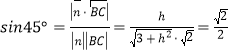 ,据此可得
,据此可得![]() ,矛盾,故直线
,矛盾,故直线![]() 与平面
与平面![]() 所成的角不可能为
所成的角不可能为![]() .
.
(1)证明:因为![]() ,
,![]() ,所以
,所以![]() 为正三角形,
为正三角形,
所以![]() ,又
,又![]() ,
,![]() 为公共边,所以
为公共边,所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
又四棱柱![]() 为直棱柱,所以
为直棱柱,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)直线![]() 与平面
与平面![]() 所成的角不可能为
所成的角不可能为![]() .
.
设![]() ,以
,以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() 如图所示,
如图所示,
不妨设![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
则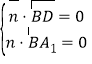 ,即
,即![]() ,
,
解得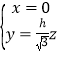 .
.
令![]() ,得
,得![]() ,
,
若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则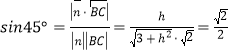 ,
,
整理得![]() ,矛盾,故直线
,矛盾,故直线![]() 与平面
与平面![]() 所成的角不可能为
所成的角不可能为![]() .
.

 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为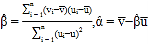 .
.
【题目】某市交管部门为了宣传新交规举办交通知识问答活动,随机对该市15~65岁的人群抽样,回答问题统计结果如图表所示.

组别 | 分组 | 回答正确的人数 | 回答正确的人数占本组的概率 |
第1组 | [15,25) | 5 | 0.5 |
第2组 | [25,35) |
| 0.9 |
第3组 | [35,45) | 27 |
|
第4组 | [45,55) |
| 0.36 |
第5组 | [55,65) | 3 |
|
(1)分别求出![]() 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.