题目内容
【题目】已知抛物线![]() 与
与
椭圆![]() 的一个交点为
的一个交点为![]() ,点
,点![]()
是![]() 的焦点,且
的焦点,且![]() .
.
(1)求![]() 与
与![]() 的方程;
的方程;
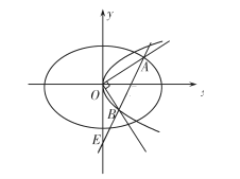
(2)设![]() 为坐标原点,在第一象限内,椭圆
为坐标原点,在第一象限内,椭圆![]() 上是否存在点
上是否存在点![]() ,使过
,使过![]() 作
作![]() 的垂线交抛物线
的垂线交抛物线![]() 于
于![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,且
,且![]() ?若存在,求出点
?若存在,求出点![]() 的坐标和
的坐标和![]() 的面积;若不存在,说明理由.
的面积;若不存在,说明理由.
【答案】(1) ![]() (2) 见解析
(2) 见解析
【解析】
(1)利用抛物线的定义求![]() ,点的坐标代入求出
,点的坐标代入求出![]() ,
,![]() 的值;
的值;
(2)设出![]() ,
,![]() 的方程与椭圆、抛物线分别联立,求出
的方程与椭圆、抛物线分别联立,求出![]() 的横坐标,利用
的横坐标,利用![]() ,即可得出结论.
,即可得出结论.
(1)由抛物线定义:![]() ,所以
,所以![]() 的方程为
的方程为![]() ,将
,将![]() 代入
代入![]() 得
得![]() ,即
,即![]() ,将
,将![]() 代入
代入![]() ,得
,得![]() ,故
,故![]() 方程为
方程为![]() .即
.即![]()
(2)由题意:直线![]() 的斜率存在且不为0,设
的斜率存在且不为0,设![]() 的方程为
的方程为![]() ,由于
,由于![]() ,则
,则![]() 的方程为
的方程为![]() ,由
,由![]() 得
得![]()
由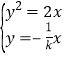 ,得
,得![]() ,得
,得![]() (舍)或
(舍)或![]()
在第一象限内,若满足![]() 的点
的点![]() 存在,则
存在,则![]() ,此时
,此时![]() ,
,
设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,由于
,由于![]() ,
,
所以![]() ,故
,故![]() ,即
,即![]() 为线段
为线段![]() 中点,
中点,
因此![]() ,即
,即![]() ,解得
,解得![]() ,
,
故存在适合题意的![]() ,此时
,此时![]() ,
,
此时![]()
![]() 方程为
方程为![]() ,即
,即![]() ,
,
点![]() 到
到![]() 的距离
的距离![]() ,
,![]() ,所以
,所以![]()

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
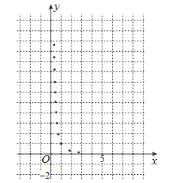
|
|
|
|
|
|
|
1.47 | 20.6 | 0.78 | 2.35 | 0.81 | -19.3 | 16.2 |
表中![]() .
.
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若旋转的弧度数![]() 与单位时间内煤气输出量
与单位时间内煤气输出量![]() 成正比,那么
成正比,那么![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为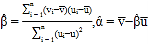 .
.