题目内容
设集合{x丨(x-1)(x2+bx+c)=0}={1,2},求b,c的值.
考点:函数的零点
专题:函数的性质及应用
分析:集合{x丨(x-1)(x2+bx+c)=0}={1,2},可得:1,2是方程(x-1)(x2+bx+c)=0的两个实数根.
因此x2+bx+c=0的实数根可能为:1,2;或有两个相等实数根2.再利用根与系数的关系即可得出.
因此x2+bx+c=0的实数根可能为:1,2;或有两个相等实数根2.再利用根与系数的关系即可得出.
解答:
解:∵集合{x丨(x-1)(x2+bx+c)=0}={1,2},
∴1,2是方程(x-1)(x2+bx+c)=0的两个实数根.
∴x2+bx+c=0的实数根可能为:1,2;或有两个相等实数根2.
①x2+bx+c=0的实数根为1,2时.
,解得b=-3,c=2.
②x2+bx+c=0有两个相等实数根2.则2+2=-b,2×2=c,解得b=-4,c=4.
∴1,2是方程(x-1)(x2+bx+c)=0的两个实数根.
∴x2+bx+c=0的实数根可能为:1,2;或有两个相等实数根2.
①x2+bx+c=0的实数根为1,2时.
|
②x2+bx+c=0有两个相等实数根2.则2+2=-b,2×2=c,解得b=-4,c=4.
点评:本题考查了一元二次方程的实数根与系数的关系,考查了分类讨论的思想方法,属于基础题.

练习册系列答案
相关题目
设
,
是两个非零向量,则下列命题正确的是( )
| a |
| b |
A、若
| ||||||||||||
B、若|
| ||||||||||||
C、若存在实数λ,使得
| ||||||||||||
D、若|
|
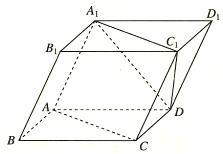 如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=∠A1AC=60°,平面AA1CC1⊥平面ABCD.
如图,棱柱ABCD-A1B1C1D1的所有棱长都等于2,∠ABC=∠A1AC=60°,平面AA1CC1⊥平面ABCD.