题目内容
6.已知f(cosx)=2cos2x,则f(sin525°)等于( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
分析 利用诱导公式得到sin525°=cos75°,再利用函数的性质能求出结果.
解答 解:∵f(cosx)=2cos2x,
∴f(sin525°)=f(sin165°)=f(sin15°)
=f(cos75°)=2cos150°=-2cos30°=-$\sqrt{3}$.
故选:D.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意诱导公式和函数性质的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
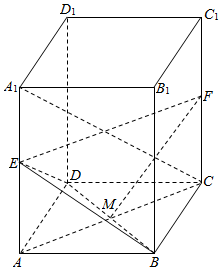 如图正四棱住ABCD-A1B1C1D1中,点E是A1A上的点,M是AC、BD的交点.
如图正四棱住ABCD-A1B1C1D1中,点E是A1A上的点,M是AC、BD的交点.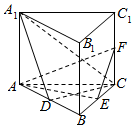 如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.
如图,直三棱柱ABC-A1B1C1的底面为正三角形,E、F分别是BC、CC1的中点.