题目内容
函数f（x）=
，则f（2）=（ ）
|
| A、-1 | B、0 | C、1 | D、2 |
考点：函数的值
专题：函数的性质及应用
分析：利用分段函数的性质求解．
解答：
解：∵函数f（x）=
，
∴f（2）=f（1）=1-2=-1．
故选：A．
|
∴f（2）=f（1）=1-2=-1．
故选：A．
点评：本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
下列各式中，正确的是（ ）
| A、（z1-z2）2+（z2-z3）2=0?z1=z2=z3 | ||||
B、|z|=1?z=
| ||||
| C、|z1+z2|=|z1|+|z2| | ||||
| D、|z|2=z2 |
设不等式|x-a|＜b解集是{x|-1＜x＜2}，则a与b的值是（ ）
| A、a=1，b=3 | ||||
| B、a=-1，b=3 | ||||
| C、a=-1，b=-3 | ||||
D、a=
|
若x1满足x+2x=4，x2满足x+log2x=4，则x1+x2=（ ）
A、
| ||
| B、3 | ||
C、
| ||
| D、4 |
函数f（x）=x2-2ax-3在区间（-8，2）上为减函数，则有（ ）
| A、a∈（-∞，1] |
| B、a∈[2，+∞） |
| C、a∈[1，2] |
| D、a∈（-∞，1]∪[2，+∞） |
（文科）已知F1、F2是椭圆
+
=1（a＞b＞0）的两个焦点，若椭圆上存在点P，满足∠F1PF2=120°，则
的取值范围是（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| b |
A、（
| ||
B、（
| ||
C、[
| ||
D、（1，
|
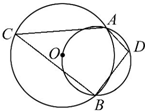如图，两圆相交于A，B两点，小圆经过大圆的圆心O，点C，D分别在两圆上，若∠ADB=100°，则∠ACB的度数为（ ）| A、35° | B、40° |
| C、50° | D、80° |
若函数f（x）=x3-2cx2+x有极值点，则实数c的范围为（ ）
A、[
| ||||||||
B、（
| ||||||||
C、（-∞，-
| ||||||||
D、（-∞，-
|