题目内容
已知函数f(x)=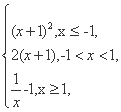 若f(a)>1,则实数a的取值范围是 .
若f(a)>1,则实数a的取值范围是 .
(-∞,-2)∪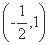

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
题目内容
已知函数f(x)=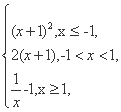 若f(a)>1,则实数a的取值范围是 .
若f(a)>1,则实数a的取值范围是 .
(-∞,-2)∪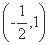

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案