题目内容
设由正数组成的等比数列,公比q=2,且a1a2…a30=230,则a3a6a9…a30等于( )
| A、210 |
| B、215 |
| C、216 |
| D、220 |
考点:等比数列的性质
专题:等差数列与等比数列
分析:由等比数列的通项公式和已知数据可得a110,而a3a6a9…a30=a1102155,代入计算可得.
解答:
解:∵正数组成的等比数列,公比q=2,且a1a2…a30=230,
∴a130•q1+2+3+…+29=a130q435=a1302435=230,
∴a130=2-405,∴a110=2-135,
∴a3a6a9…a30=a110•q2+5+8+…+29=a1102155
=2-135•2155=220,
故选:D
∴a130•q1+2+3+…+29=a130q435=a1302435=230,
∴a130=2-405,∴a110=2-135,
∴a3a6a9…a30=a110•q2+5+8+…+29=a1102155
=2-135•2155=220,
故选:D
点评:本题考查等比数列的性质,属基础题.

练习册系列答案
相关题目
| ∫ | 2 1 |
| 1 |
| x |
| A、1 | B、2 | C、ln2 | D、-ln2 |
在△ABC中,角A、B的对边分别为a、b且A=2B,则
的取值范围是( )
| a |
| b |
A、(0,
| ||
| B、(1,2) | ||
C、(
| ||
| D、(0,2) |
平面α的一个法向量为(1,2,0),平面β的一个法向量为(2,-1,0),则平面α与平面β的位置关系是( )
| A、平行 | B、相交但不垂直 |
| C、垂直 | D、不能确定 |
各项均为正数的数列{an},{bn}满足:an+2=2an+1+an,bn+2=bn+1+2bn(n∈N*),那么( )
| A、?n∈N*,an>bn⇒an+1>bn+1 |
| B、?m∈N*,?n>m,an=bn |
| C、?m∈N*,?n>m,an>bn |
| D、?m∈N*,?n>m,an<bn |
以椭圆C:
+
=1的焦点为顶点,以椭圆C的顶点为焦点的双曲线的方程是( )
| x2 |
| 8 |
| y2 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
抛物线y2=4x的焦点为F,M为抛物线上的动点,又已知点N(-1,0),则
的取值范围是( )
| |MN| |
| |MF| |
A、[1,2
| ||||
B、[
| ||||
C、[
| ||||
D、[1,
|
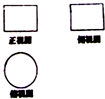 如图所示的是一个立体图形的三视图,此立体图形的名称为:
如图所示的是一个立体图形的三视图,此立体图形的名称为: