题目内容
已知三个点A(2,1),B(3,2),D(-1,4).
(1)求证: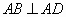 ;
;
(2)要使四边形ABCD为矩形,求点C的坐标,并求矩形ABCD的两对角线所夹的锐角的余弦值.
答案:略
解析:
提示:
解析:
|
(1)证明:∵A(2,1),B(3,2),D(-1,4),∴ 又∵ ∴ (2)解:∵ 设C点坐标为(x,y),则 ∴ 从而
设 ∴求得矩形的两条对角线所成的锐角的余弦值为 |
提示:
|
要证明  ,只需证 ,只需证 .在 .在 的前提下,只要找点C使 的前提下,只要找点C使 .而由两向量夹角的余弦值可以得到两对角线所夹锐角的余弦值. .而由两向量夹角的余弦值可以得到两对角线所夹锐角的余弦值. |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, .
. ,
, .
. ,
, 解得
解得 ∴C点坐标为(0,5).
∴C点坐标为(0,5). ,
, ,且
,且 ,
, .
. ,
, 与
与 夹角为
夹角为 ,则
,则 ,
, .
. ;
;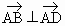 ;
;