题目内容
已知数列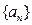 中,
中,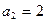 ,前
,前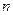 项和为
项和为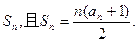
(I)证明数列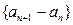 是等差数列,并求出数列
是等差数列,并求出数列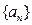 的通项公式;
的通项公式;
(II)设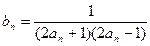 ,数列
,数列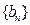 的前
的前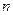 项和为
项和为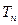 ,求使不等式
,求使不等式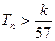 对一切
对一切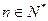 都成立的最大正整数
都成立的最大正整数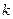 的值。
的值。
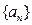 中,
中,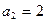 ,前
,前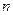 项和为
项和为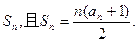
(I)证明数列
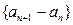 是等差数列,并求出数列
是等差数列,并求出数列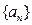 的通项公式;
的通项公式;(II)设
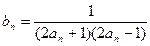 ,数列
,数列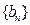 的前
的前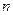 项和为
项和为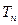 ,求使不等式
,求使不等式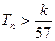 对一切
对一切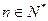 都成立的最大正整数
都成立的最大正整数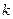 的值。
的值。(1)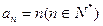 (2)
(2)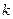 的最大值为18。
的最大值为18。
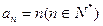 (2)
(2)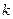 的最大值为18。
的最大值为18。(1)由题意,当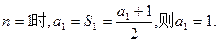
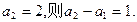
当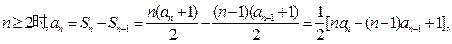
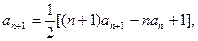
则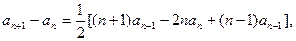
则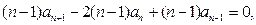
即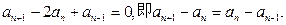
则数列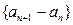 是首项为1,公差为0的等差数列。
是首项为1,公差为0的等差数列。
从而 ,则数列
,则数列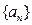 是首项为1,公差为1的等差数列。
是首项为1,公差为1的等差数列。
所以,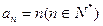
(2)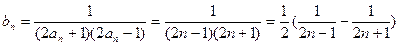
所以,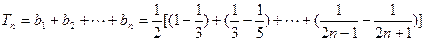
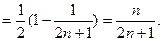
由于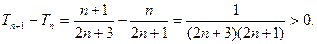
因此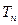 单调递增,故
单调递增,故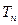 的最小值为
的最小值为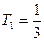
令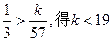 ,所以
,所以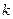 的最大值为18。
的最大值为18。
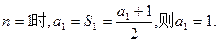
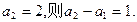
当
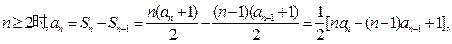
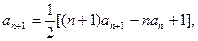
则
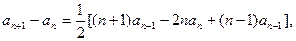
则
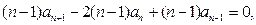
即
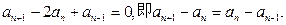
则数列
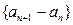 是首项为1,公差为0的等差数列。
是首项为1,公差为0的等差数列。从而
 ,则数列
,则数列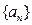 是首项为1,公差为1的等差数列。
是首项为1,公差为1的等差数列。所以,
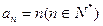
(2)
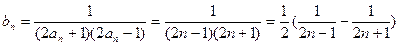
所以,
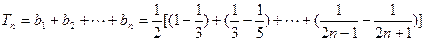
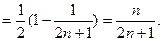
由于
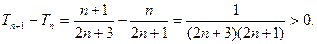
因此
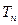 单调递增,故
单调递增,故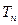 的最小值为
的最小值为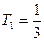
令
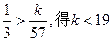 ,所以
,所以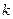 的最大值为18。
的最大值为18。
练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
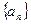 的前n项之和为Sn,令
的前n项之和为Sn,令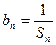 ,且
,且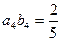 ,S6-S3=15.
,S6-S3=15.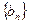 的通项公式与它的前10项之和;
的通项公式与它的前10项之和;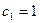 ,
,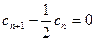 ,
,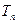 =
=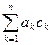 ,求
,求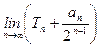 的值.
的值.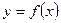 的图像是自原点出发的一条折线,当
的图像是自原点出发的一条折线,当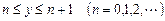 时,该图像是斜率为
时,该图像是斜率为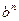 的线段(其中正常数
的线段(其中正常数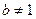 ),设数列
),设数列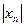 由
由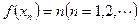 定义.
定义.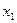 、
、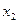 和
和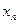 的表达式;
的表达式;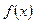 的表达式,并写出其定义域;
的表达式,并写出其定义域;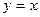 的图像没有横坐标大于1的交点.
的图像没有横坐标大于1的交点.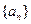 的前
的前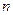 项和为
项和为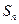 ,若
,若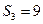 ,
,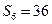 ,则
,则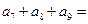 ( )
( ) , 设an= g(n)-g(n-1) (n∈N※), 则数列{an}是 ( )
, 设an= g(n)-g(n-1) (n∈N※), 则数列{an}是 ( )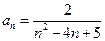 则{an}的最大项是
则{an}的最大项是
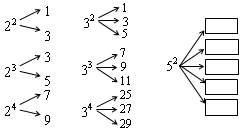
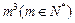 的“分裂”
的“分裂”