题目内容
已知函数f(x)＝
＋
cos 2x－m，若f(x)的最大值为1.
(1)求m的值，并求f(x)的单调递增区间；
(2)在△ABC中，角A、B、C的对边分别为a、b、c，若f(B)＝－1，且a＝b＋c，试判断三角形的形状．
解：(1)f(x)＝2sin 2x·cos
＋cos 2x－m＝sin 2x＋cos 2x－m＝2sin
－m.
又f(x)max＝2－m，所以2－m＝1，得m＝1.
又a＝b＋c，则sin A＝sin B＋sin C，
故△ABC为直角三角形．
练习册系列答案
相关题目
,n是正整数，假设n=k时，等式成立，则当n=k+1时，应推证的目标等式是_____________.
＝_____________________________.
＝3
，点O在线段CD上(与点C、D不重合)，若
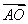＝x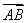
＋(1－x)
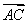，则x的取值范围是( )
＝________.
＋
＋
＝0.若存在实数m使得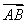
＋
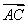＝m
成立，则m＝________. 
，
，
，
，…，
(m≥7，且m∈N*)．