题目内容
数列 的通项公式为
的通项公式为 ,等比数列
,等比数列 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(1) ; (2)
; (2)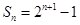 ;(3)
;(3)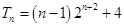
解析试题分析:(1)求等比数列通项,一般方法为待定系数法,设公比为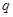 ,利用条件
,利用条件 列出关于
列出关于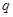 的方程:
的方程: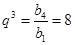 ,
,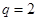 ,代入通项公式即可:
,代入通项公式即可: ;(2)利用等比数列前
;(2)利用等比数列前 项和
项和 公式:
公式: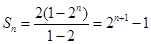 ;注意代公式时的前提条件;
;注意代公式时的前提条件; ,而而
,而而 时,
时,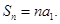 (3)数列
(3)数列 通项为“等比乘等差”型,所以求和用“错位相减法”, 令
通项为“等比乘等差”型,所以求和用“错位相减法”, 令 ,则
,则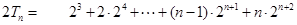 ,两式相减得
,两式相减得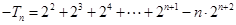
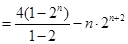 所以,
所以,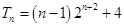 ,用“错位相减法”求和很容易出错,须注意三个方面,一是两式相减时,项的符号变化,二是中间求和时,须明确项的个数,三是最后须除以
,用“错位相减法”求和很容易出错,须注意三个方面,一是两式相减时,项的符号变化,二是中间求和时,须明确项的个数,三是最后须除以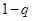 ,才可得到最后结果.
,才可得到最后结果.
试题解析:
(I)由已知,得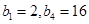 ,
,
且数列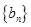 为等比数列,设公比为
为等比数列,设公比为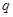 ,则
,则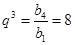 , 1分
, 1分
解得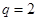 , 2分
, 2分
则数列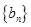 的通项公式为
的通项公式为 ; 3分
; 3分
(II)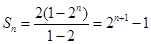 ; 6分
; 6分
(III)由已知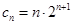 ,
,
所以,  . ① 7分
. ① 7分 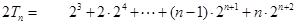 ②8分
②8分
①-②,得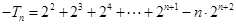 10分
10分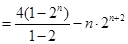
所以,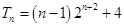 12分
12分
考点:等比数列通项及和项,错位相减法求和

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来
;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来 的线段,且这两条线段与原线段两两夹角为
的线段,且这两条线段与原线段两两夹角为 级分形图.
级分形图.
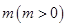 万吨.
万吨.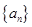 ,求相邻两年主要污染物排放总量的关系式;
,求相邻两年主要污染物排放总量的关系式;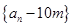 是等比数列;
是等比数列;
 改选B菜;而选B菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有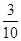 改选A菜。用
改选A菜。用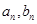 分别表示第
分别表示第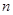 个星期选A的人数和选B的人数.
个星期选A的人数和选B的人数.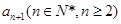 表示
表示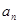 ,判断数列
,判断数列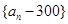 是否成等比数列并说明理由;
是否成等比数列并说明理由; 的前
的前 项和为
项和为 满足
满足 .
. 的前
的前 .
.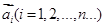 排成一列,称为向量列,记作
排成一列,称为向量列,记作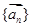 ,又设
,又设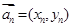 ,假设向量列
,假设向量列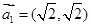 ,
,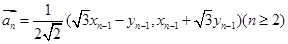 。
。 是等比数列;
是等比数列;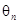 表示向量
表示向量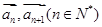 间的夹角,若
间的夹角,若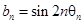 ,记
,记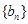 的前
的前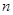 项和为
项和为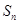 ,求
,求 ;
;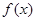 是
是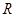 上不恒为零的函数,且对任意的
上不恒为零的函数,且对任意的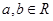 ,都有
,都有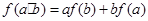 ,若
,若 ,
,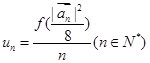 ,求数列
,求数列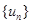 的前
的前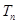 .
.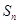 表示数列
表示数列 的前
的前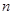 项和.
项和.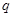 的等比数列,写出并推导
的等比数列,写出并推导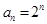 ,
,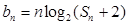 ,求证:
,求证: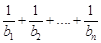 <1.
<1.