题目内容
已知a＞b＞0，求证：a+
＞b+
．
| 1 |
| b |
| 1 |
| a |
分析：直接利用作差法，判断a+
，b+
两个数值的差的大小，即可证明不等式成立．
| 1 |
| b |
| 1 |
| a |
解答：证明：由于a+
-（b+
）=（a-b）+（
-
）
=（a-b）（1+
）=（a-b）•
，
因为a＞b＞0⇒ab＞0⇒ab+1＞0且a-b＞0，
所以（a-b）•
＞0．
即a+
-（b+
）＞0．
所以a＞b＞0时，a+
＞b+
成立．
| 1 |
| b |
| 1 |
| a |
| 1 |
| b |
| 1 |
| a |
=（a-b）（1+
| 1 |
| ab |
| ab+1 |
| ab |
因为a＞b＞0⇒ab＞0⇒ab+1＞0且a-b＞0，
所以（a-b）•
| ab+1 |
| ab |
即a+
| 1 |
| b |
| 1 |
| a |
所以a＞b＞0时，a+
| 1 |
| b |
| 1 |
| a |
点评：本题主要考查不等式的证明方法：作差法的应用，本题也可以利用分析法证明．
练习册系列答案
相关题目
-
＜
；
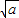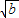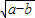，b=y2-2z+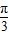
，c=z2-2x+
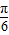求证：a，b，c中至少有一个大于0．