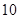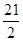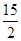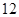题目内容
如图,边长为1的正方形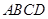 的顶点
的顶点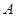 ,
,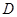 分别在
分别在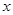 轴、
轴、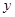 轴正半轴上移动,则
轴正半轴上移动,则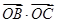 的最大值是( )
的最大值是( )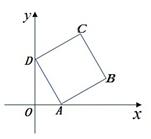
A.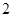 | B.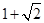 | C.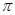 | D.4 |
A
解析试题分析:如图令 ,由于
,由于 故
故 ,
, ,
,
如图 ,AB=1,故
,AB=1,故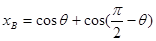
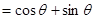 ,
, ,故
,故 ,
,
同理可求得 ,所以
,所以 ,
,
所以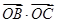 的最大值为2.
的最大值为2.
考点:平面向量数量积坐标表示的应用.
点评:本题考查向量在几何中的应用,设角引入坐标是解题的关键,由于向量的运算与坐标关系密切,所以在研究此类题时应该想到设角来表示点的坐标,属于中档题

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知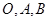 是平面上的三个点,直线
是平面上的三个点,直线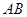 上有一点
上有一点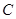 满足
满足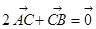 ,则
,则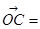 ( )
( )
A. | B. | C.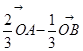 | D.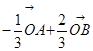 |
若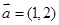 ,
, ,
, ,则
,则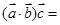
A. | B. | C. | D.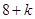  |
已知向量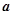 、
、 的夹角为
的夹角为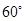 ,且
,且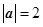 ,
,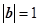 ,则向量
,则向量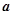 与向量
与向量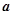 +2
+2 的夹角等于( )
的夹角等于( )
| A.150° | B.90° | C.60° | D.30° |
若 ( )
( )
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.以上答案均有可能 |
已知a,b是平面内两个互相垂直的单位向量,若向量c满足(a-c)·(b一c)=0,则|c|的最大值是
| A.1 | B. | C.2 | D. |
设向量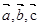 ,满足
,满足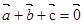 ,且
,且 ,
, ,则
,则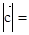 ( ).
( ).
| A.1 | B. | C.2 | D.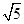 |
若 是夹角为
是夹角为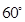 的两个单位向量,则
的两个单位向量,则 的夹角为
的夹角为
A. | B. | C. | D. |