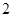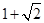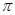题目内容
在梯形ABCD中,AD//BC,对角线AC⊥BD,且AC=12,BD=9,则此梯形的
中位线长是( ).
A.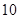 | B.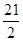 | C.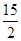 | D.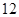 |
C
解析试题分析:过点D作 ,交BC于点E,
,交BC于点E,
所以可得DE=AC,AD=CE,又因为 ,所以BD⊥DE,根据勾股定理,
,所以BD⊥DE,根据勾股定理, ,而梯形的中位线等于上底与下底的和的一半,所以梯形的中位线长为
,而梯形的中位线等于上底与下底的和的一半,所以梯形的中位线长为
考点:本小题主要考查梯形边角之间的数量关系的应用.
点评:解决本小题的关键是作辅助线 ,进而就可以利用数量关系和勾股定理进行求解.
,进而就可以利用数量关系和勾股定理进行求解.

练习册系列答案
相关题目
已知a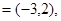 b=
b=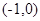 ,向量
,向量 垂直,则实数
垂直,则实数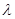 的值为( )
的值为( )
A.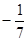 | B.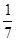 | C.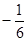 | D.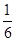 |
在直角三角形 中,
中, ,
, ,取点
,取点 ,
, 使
使 ,那么
,那么 =( )
=( )
| A.3 | B. 6 | C. | D. |
已知a, b均为单位向量,它们的夹角为 ,那么|a+3b|=( )
,那么|a+3b|=( )
A. | B. | C. | D. |
向量 在向量
在向量 上的投影是( )
上的投影是( )
A. | B. | C. | D. |
设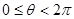 ,已知两个向量
,已知两个向量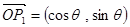 ,
,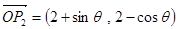 ,则向量
,则向量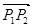 长度的最大值是( )
长度的最大值是( )
A.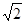 | B.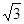 | C.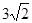 | D.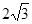 |
已知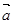 与
与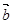 的夹角为
的夹角为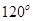 ,
,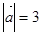 ,
,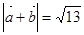 ,则
,则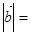 ( )
( )
| A.5 | B.4 | C.3 | D.1 |
如图在四边形 中,设
中,设 ,
, ,
, ,则
,则

A. | B. |
C. | D. |
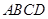 的顶点
的顶点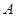 ,
,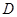 分别在
分别在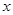 轴、
轴、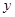 轴正半轴上移动,则
轴正半轴上移动,则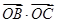 的最大值是( )
的最大值是( )