题目内容
在锐角△ABC中,角A、B、C所对的边分别为a、b、c,且
=
.
(Ⅰ)求角A;
(Ⅱ)若a=2,求△ABC的面积的最大值.
| b2-a2-c2 |
| ac |
| cos(A+C) |
| sinAcosA |
(Ⅰ)求角A;
(Ⅱ)若a=2,求△ABC的面积的最大值.
考点:余弦定理
专题:解三角形
分析:(Ⅰ)已知等式左边利用余弦定理化简,右边分子利用诱导公式化简,分母利用二倍角的正弦函数公式化简,根据cosB不为0求出sin2A的值,即可确定出角A的度数;
(Ⅱ)利用三角形面积公式表示出S,把sinA的值代入,由a与cosA的值,利用余弦定理列出关系式,并利用基本不等式求出bc的最大值,即可确定出三角形面积的最大值.
(Ⅱ)利用三角形面积公式表示出S,把sinA的值代入,由a与cosA的值,利用余弦定理列出关系式,并利用基本不等式求出bc的最大值,即可确定出三角形面积的最大值.
解答:
解:(Ⅰ)∵
=
,
∴-2cosB=
,
∵B是锐角,∴cosB≠0,
∴sin2A=1,
∵0<A<
,即0<2A<π,
∴2A=
,即A=
;
(Ⅱ)∵sinA=
,
∴S△ABC=
bcsinA=
bc,
∵a=2,cosA=
,
∴由余弦定理得:22=b2+c2-2bc×
≥2bc-
bc,
∴(2-
)bc≤4,即bc≤2(2+
),
∴S△ABC=
bc≤
×2(2+
)=
+1,
∴S△ABC的面积的最大值为
+1.
| b2-a2-c2 |
| ac |
| cos(A+C) |
| sinAcosA |
∴-2cosB=
| -2cosB |
| sin2A |
∵B是锐角,∴cosB≠0,
∴sin2A=1,
∵0<A<
| π |
| 2 |
∴2A=
| π |
| 2 |
| π |
| 4 |
(Ⅱ)∵sinA=
| ||
| 2 |
∴S△ABC=
| 1 |
| 2 |
| ||
| 4 |
∵a=2,cosA=
| ||
| 2 |
∴由余弦定理得:22=b2+c2-2bc×
| ||
| 2 |
| 2 |
∴(2-
| 2 |
| 2 |
∴S△ABC=
| ||
| 4 |
| ||
| 4 |
| 2 |
| 2 |
∴S△ABC的面积的最大值为
| 2 |
点评:此题考查了余弦定理,三角形面积公式,以及特殊角的三角函数值,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
一个几何体的三视图如图所示,且其侧(左)视图是一个等边三角形,则这个几何体的体积为( )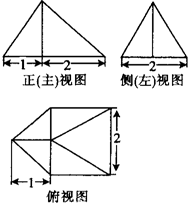

A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
某单位共有老、中、青职工860人,其中青年职工320人,中年职工人数是老年职工人数的2倍.为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中有青年职工64人,则该样本中的老年职工人数为 .
已知M(x0,y0)是圆x2+y2=a2外任意一点,则直线x0x+y0y=a2与该圆的位置关系是( )
| A、相切 |
| B、相交 |
| C、相离 |
| D、由点(x0、y0)的位置决定 |
在函数y=x3,y=2x,y=log2x,y=
中,奇函数的是( )
| x |
| A、y=x3 | ||
| B、y=2x | ||
| C、y=log2x | ||
D、y=
|

 如图,有一块扇形草地OMN,已知半径为R,
如图,有一块扇形草地OMN,已知半径为R,