题目内容
1.在△ABC中,角A、B、C所对的边分别为a、b、c,已知向量$\overrightarrow{m}$=(cosA,cosB),$\overrightarrow{n}$=(b+2c,a),且$\overrightarrow{m}$⊥$\overrightarrow{n}$.(1)求角A的大小;
(2)若a=4$\sqrt{3}$,b+c=8,求AC边上的高h的大小.
分析 (1)根据$\overrightarrow{m}$⊥$\overrightarrow{n}$时$\overrightarrow{m}$•$\overrightarrow{n}$=0,由正弦定理与两角和的正弦公式、内角和定理求出cosA=-$\frac{1}{2}$,即可求得A的值;
(2)由余弦定理和已知条件求出b=c=4,再求AC边上的高h.
解答 解:(1)△ABC中,向量$\overrightarrow{m}$=(cosA,cosB),$\overrightarrow{n}$=(b+2c,a),且$\overrightarrow{m}$⊥$\overrightarrow{n}$,
∴$\overrightarrow{m}$•$\overrightarrow{n}$=(b+2c)cosA+acosB=0,
由正弦定理得(sinB+2sinC)cosA+sinAcosB=0,
∴sinBcosA+cosBsinA+2sinCcosA=0,
∴sin(A+B)+2sinCcosA=0,
即sinC+2sinCcosA=0;
又C∈(0,π),∴sinC≠0,
∴cosA=-$\frac{1}{2}$;
又A∈(0,π),∴A=$\frac{2π}{3}$;
(2)若a=4$\sqrt{3}$,b+c=8,
∴a2=b2+c2-2bccosA=b2+c2-2bccos$\frac{2π}{3}$=b2+c2+bc=48;
又(b+c)2=b2+c2+2bc=64,
∴bc=16;
解得b=c=4,
∴AC边上的高为h=4•sin(π-$\frac{2π}{3}$)=2$\sqrt{3}$.
点评 本题考查了平面向量数量积与解三角形的应用问题,也考查了三角恒等变换问题,是综合题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
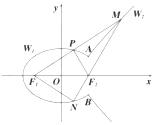 如图:椭圆$\frac{x^2}{2}+{y^2}$=1与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)有相同的焦点F1、F2,它们在y轴右侧有两个交点A、B,满足$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}$=0.将直线AB左侧的椭圆部分(含A,B两点)记为曲线W1,直线AB右侧的双曲线部分(不含A,B两点)记为曲线W2.以F1为端点作一条射线,分别交W1于点P(xP,yP),交W2于点M(xM,yM)(点M在第一象限),设此时$\overrightarrow{{F_1}M}=m•\overrightarrow{{F_1}P}$.
如图:椭圆$\frac{x^2}{2}+{y^2}$=1与双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)有相同的焦点F1、F2,它们在y轴右侧有两个交点A、B,满足$\overrightarrow{{F_2}A}+\overrightarrow{{F_2}B}$=0.将直线AB左侧的椭圆部分(含A,B两点)记为曲线W1,直线AB右侧的双曲线部分(不含A,B两点)记为曲线W2.以F1为端点作一条射线,分别交W1于点P(xP,yP),交W2于点M(xM,yM)(点M在第一象限),设此时$\overrightarrow{{F_1}M}=m•\overrightarrow{{F_1}P}$.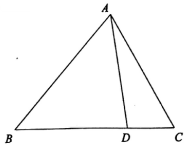 在△ABC中,D为BC边上一点,AD=BD,AC=4,BC=5.
在△ABC中,D为BC边上一点,AD=BD,AC=4,BC=5.