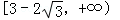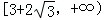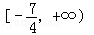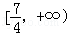题目内容
设双曲线 =1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为
=1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为
A. | B.5 | C. | D. |
D
解析试题分析:双曲线 =1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,
=1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点, =1的渐近线方程为
=1的渐近线方程为 ,不妨将
,不妨将 代入y=x2+1整理得, x2-
代入y=x2+1整理得, x2- +1=0,由
+1=0,由 =
=  得,
得, =4,
=4, ,故选D。
,故选D。
考点:本题主要考查双曲线的几何性质,直线与抛物线的位置关系。
点评:典型题,涉及圆锥曲线的几何性质问题,往往涉及a,b,c,e的关系,应熟记。

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
椭圆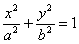
 的离心率是
的离心率是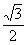 ,则双曲线
,则双曲线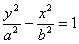 的渐近线方程是( )
的渐近线方程是( )
A.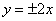 | B.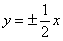 | C.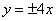 | D.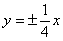 |
过双曲线的一个焦点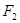 作垂直于实轴的弦
作垂直于实轴的弦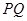 ,
,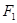 是另一焦点,若∠
是另一焦点,若∠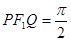 ,则双曲线的离心率
,则双曲线的离心率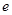 等于( )
等于( )
A. | B.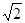 | C.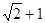 | D.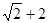 |
抛物线 的焦点为
的焦点为 ,点
,点 在抛物线上,且
在抛物线上,且 ,弦
,弦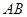 中点
中点 在准线
在准线 上的射影为
上的射影为 的最大值为( )
的最大值为( )
A. | B. | C. | D. |
已知 ,
,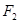 是椭圆
是椭圆 的两个焦点,焦距为4.若
的两个焦点,焦距为4.若 为椭圆
为椭圆 上一点,且
上一点,且 的周长为14,则椭圆
的周长为14,则椭圆 的离心率
的离心率 为
为
A.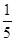 | B. | C. | D. |
 分别为双曲线
分别为双曲线 (a>0,b>0)的左、右焦点,O为原点,A为右顶点,
(a>0,b>0)的左、右焦点,O为原点,A为右顶点,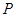 为双曲线左支上的任意一点,若
为双曲线左支上的任意一点,若 存在最小值为12a,则双曲线离心率
存在最小值为12a,则双曲线离心率 的取值范围是( )
的取值范围是( )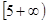
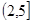


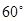 的直线交椭圆于A、B两点,若
的直线交椭圆于A、B两点,若 ,则椭圆的离心率为( )
,则椭圆的离心率为( ) B.
B.  C.
C.  D.
D. 
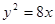 相切倾斜角为
相切倾斜角为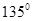 的直线L与x轴和y轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线
的直线L与x轴和y轴的交点分别是A和B,那么过A、B两点的最小圆截抛物线 C.2 D.
C.2 D.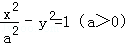 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则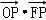 的取值范围为
的取值范围为