题目内容
5.设函数y=f(x)定义域为D,若对于任意x1,x2∈D且x1+x2=2a,恒有f(x1)+f(x2)=2b,则称点(a,b)为函数y=f(x)图象的对称中心.研究并利用函数f(x)=x3-3x2-sin(πx)的对称中心,计算$S=f(\frac{1}{2015})+f(\frac{2}{2015})+…+f(\frac{4028}{2015})+f(\frac{4029}{2015})$的值( )| A. | -8058 | B. | 8058 | C. | -8060 | D. | 8060 |
分析 观察到自变量前后对称相加和为定值2,故令a=1,x1+x2=2,求得f(x1)+f(x2)=-4,从而求得要求式子的值.
解答 解:观察到自变量前后对称相加和为定值2,故令a=1,∵x1+x2=2,
∴$f({x_1})+f({x_2})={x_1}^3-3{x_1}^2-sin(π{x_1})+{(2-{x_1})^3}-3{(2-{x_1})^2}-sin[π(2-{x_1})]=-4$,为定值,
∴$S=f(\frac{4029}{2015})+f(\frac{4028}{2015})+…+f(\frac{2}{2015})+f(\frac{1}{2015})$,
故2S=-4×4029,∴S=-8058.
故选:A.
点评 本题主要考查正弦函数的函数的图象的对称性,求函数的值,属于中档题.

练习册系列答案
相关题目
10.若图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则这个几何体外接球的表面积为( )
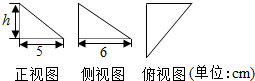

| A. | 25xcm2 | B. | $\frac{77π}{2}$cm2 | C. | 77πcm2 | D. | 144πcm2 |
13.设x>0,则“a=1”是“x+$\frac{a}{x}$≥2恒成立”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
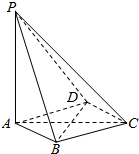 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.