题目内容
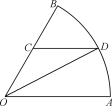
【题目】如图1,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() ,过
,过![]() 作
作![]() 交
交![]() 于
于![]() ,现将
,现将![]() 沿
沿![]() 折到
折到![]() ,使
,使![]() ,如图2.
,如图2.
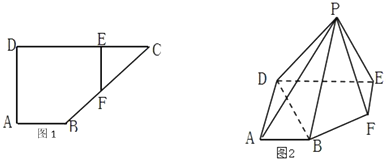
(1)求证:![]() 平面
平面![]()
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?若存在,确定点
?若存在,确定点![]() 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
【答案】(1)证明见解析;(2)不存在,理由见解析
【解析】
(1)解法一:由![]() ,
,![]() ,推出
,推出![]() 平面
平面![]() ,即有
,即有![]() 平面
平面![]() ,故
,故![]() ,结合
,结合![]() 即可推出
即可推出![]() 平面
平面![]() ;解法二:建立空间直角坐标系,利用向量推出结论;
;解法二:建立空间直角坐标系,利用向量推出结论;
(2)由(1)知![]() 平面
平面![]() ,故以
,故以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]() 轴,在平面
轴,在平面![]() 内过
内过![]() 作
作![]() 的垂线,以垂线所在直线为
的垂线,以垂线所在直线为![]() 轴,建立空间直角坐标系,设
轴,建立空间直角坐标系,设![]() 是线段
是线段![]() 上一点,则存在
上一点,则存在![]() ,使
,使![]() ,再利用向量,结合线面角公式列式求解即可.
,再利用向量,结合线面角公式列式求解即可.
(1)解法一:
∵![]() ,
,![]() ,
,![]() ,
,
由余弦定理得![]() ,
,
∵![]() ,∴
,∴![]() ,
,
又直角梯形![]() 中,
中,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
则![]() 平面
平面![]() ,
,
又∵![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又因为直线![]() ,
,![]() 在平面
在平面![]() 内,且相交于
内,且相交于![]() ,∴
,∴![]() 平面
平面![]() .
.
解法二:
以为![]() ,
,![]() ,且
,且![]() ,
,
则![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,
以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]() 轴,在平面
轴,在平面![]() 内过
内过![]() 作
作![]()
的垂线,以垂线所在直线为![]() 轴,建立空间直角坐标系,如图所示:
轴,建立空间直角坐标系,如图所示:
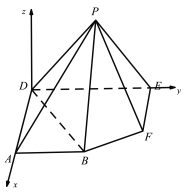
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]()
∴![]() ,
,![]() ,
,
∵![]() ,
,![]() 是平面
是平面![]() 内的相交直线,
内的相交直线,
∴![]() 平面
平面![]() .
.
(2)由(1)知![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
以![]() 所在的直线为
所在的直线为![]() 轴,以
轴,以![]() 所在的直线为
所在的直线为![]() 轴,在平面
轴,在平面![]() 内过
内过![]() 作
作![]() 的垂线,以垂线所在直线为
的垂线,以垂线所在直线为![]() 轴,建立空间直角坐标系,如图所示:
轴,建立空间直角坐标系,如图所示:
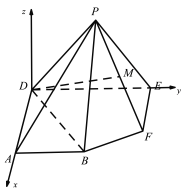
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设![]() 是线段
是线段![]() 上一点,则存在
上一点,则存在![]() ,使
,使![]() ,
,
∴![]()
![]() ,
,
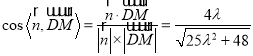 ,
,
如果直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
那么![]() ,即
,即![]() ,
,
解得![]() ,此方程在
,此方程在![]() 内无解,
内无解,
所以在线段![]() 上不存在一点
上不存在一点![]() ,使
,使![]() 与平在
与平在![]() 所成的角为
所成的角为![]() .
.

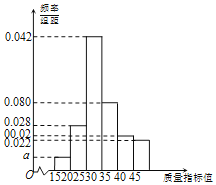
【题目】为保障食品安全,某地食品药监管部门对辖区内甲、乙两家食品企业进行检查,分别从这两家企业生产的某种同类产品中随机抽取了100件作为样本,并以样本的一项关键质量指标值为检测依据.已知该质量指标值对应的产品等级如下:
质量指标值 | [15,20) | [20,25) | [25,30) | [30,35) | [35,40) | [40,45] |
等级 | 次品 | 二等品 | 一等品 | 二等品 | 三等品 | 次品 |
根据质量指标值的分组,统计得到了甲企业的样本频率分布直方图和乙企业的样本频数分布表(如下面表,其中a>0).
质量指标值 | 频数 |
[15,20) | 2 |
[20,25) | 18 |
[25,30) | 48 |
[30,35) | 14 |
[35,40) | 16 |
[40,45] | 2 |
合计 | 100 |
(Ⅰ)现从甲企业生产的产品中任取一件,试估计该件产品为次品的概率;
(Ⅱ)为守法经营、提高利润,乙企业开展次品生产原因调查活动.已知乙企业从样本里的次品中随机抽取了两件进行分析,求这两件次品中恰有一件指标值属于[40,45]的产品的概率;
(Ⅲ)根据图表数据,请自定标准,对甲、乙两企业食品质量的优劣情况进行比较.