题目内容
【题目】要排出高三某班一天中，语文、数学、英语各
节，自习课
节的功课表，其中上午
节，下午节，若要求节语文课必须相邻且节数学课也必须相邻（注意：上午第五节和下午第一节不算相邻），则不同的排法种数是（ ）
A.
B.
C.
D.
【答案】C
【解析】
根据题意，分两种情况进行讨论：①语文和数学都安排在上午；②语文和数学一个安排在上午，一个安排在下午.分别求出每一种情况的安排方法数目，由分类加法计数原理可得答案．
根据题意，分两种情况进行讨论：
①语文和数学都安排在上午，要求
节语文课必须相邻且节数学课也必须相邻，将节语文课和节数学课分别捆绑，然后在剩余
节课中选
节到上午，由于节英语课不加以区分，此时，排法种数为
种；
②语文和数学都一个安排在上午，一个安排在下午.
语文和数学一个安排在上午，一个安排在下午，但节语文课不加以区分，节数学课不加以区分，节英语课也不加以区分，此时，排法种数为
种.
综上所述，共有
种不同的排法.
故选：C．
练习册系列答案
口算能手系列答案
相关题目
【题目】某校高三期中考试后，数学教师对本次全部学生的数学成绩按1∶20进行分层抽样，随机抽取了20名学生的成绩为样本，成绩用茎叶图记录如图所示，但部分数据不小心丢失，同时得到如下表所示的频率分布表：
分数段（分） |
|
|
|
|
| 总计 |
频数 |
| |||||
频率 |
| 0.25 |
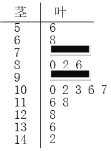
（1）求表中
，
的值及成绩在
范围内的样本数；
（2）从成绩
内的样本中随机抽取4个样本，设其中成绩在
内的样本个数为随机变量
，求的分布列及数学期望
；
（3）若把样本各分数段的频率看作总体相应各分数段的概率，现从全校高三期中考试数学成绩中随机抽取5个，求其中恰有2个成绩在
内的概率.
