МвДїДЪИЭ
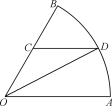
ЎѕМвДїЎїИзНјКЗТ»ёц°лѕ¶ОЄ2З§ГЧЈ¬ФІРДЅЗОЄ![]() µДЙИРОУОААЗшµДЖЅГжКѕТвНј
µДЙИРОУОААЗшµДЖЅГжКѕТвНј![]() КЗ°лѕ¶
КЗ°лѕ¶![]() ЙПТ»µгЈ¬
ЙПТ»µгЈ¬![]() КЗФІ»Ў
КЗФІ»Ў![]() ЙПТ»µгЈ¬ЗТ
ЙПТ»µгЈ¬ЗТ![]() .ПЦФЪПЯ¶О
.ПЦФЪПЯ¶О![]() Ј¬ПЯ¶О
Ј¬ПЯ¶О![]() ј°ФІ»Ў
ј°ФІ»Ў![]() Иэ¶ОЛщКѕО»ЦГЙиБў№гёжО»Ј¬ѕІвЛг№гёжО»іцЧвКХИлКЗЈєПЯ¶О
Иэ¶ОЛщКѕО»ЦГЙиБў№гёжО»Ј¬ѕІвЛг№гёжО»іцЧвКХИлКЗЈєПЯ¶О![]() ґ¦ГїЗ§ГЧОЄ
ґ¦ГїЗ§ГЧОЄ![]() ФЄЈ¬ПЯ¶О
ФЄЈ¬ПЯ¶О![]() ј°ФІ»Ў
ј°ФІ»Ў![]() ґ¦ГїЗ§ГЧѕщОЄ
ґ¦ГїЗ§ГЧѕщОЄ![]() ФЄЈ®Йи
ФЄЈ®Йи![]() »Ў¶ИЈ¬№гёжО»іцЧвµДЧЬКХИлОЄ
»Ў¶ИЈ¬№гёжО»іцЧвµДЧЬКХИлОЄ![]() ФЄЈ®
ФЄЈ®
(1)Зу![]() №ШУЪ
№ШУЪ![]() µДєЇКэЅвОцКЅЈ¬ІўЦёіцёГєЇКэµД¶ЁТеУтЈ»
µДєЇКэЅвОцКЅЈ¬ІўЦёіцёГєЇКэµД¶ЁТеУтЈ»
(2)КФОКЈє![]() ОЄєОЦµК±Ј¬№гёжО»іцЧвµДЧЬКХИлЧоґуЈїІўЗуіцЖдЧоґуЦµЈ®
ОЄєОЦµК±Ј¬№гёжО»іцЧвµДЧЬКХИлЧоґуЈїІўЗуіцЖдЧоґуЦµЈ®
Ўѕґр°ёЎїЈЁ1Ј©![]() Ј»ЈЁ2Ј©µ±
Ј»ЈЁ2Ј©µ±![]() К±Ј¬№гёжО»іцЧвµДЧЬКХИлЧоґуЈ¬ЧоґуЦµОЄ
К±Ј¬№гёжО»іцЧвµДЧЬКХИлЧоґуЈ¬ЧоґуЦµОЄ![]() ФЄ.
ФЄ.
ЎѕЅвОцЎї
ЈЁ1Ј©ёщѕЭМвТвЈ¬АыУГХэПТ¶ЁАнЗуµГOCµДЦµЈ¬ФЩЗу»Ўі¤DBЈ¬ЗуіцєЇКэyµДЅвОцКЅЈ¬РґіцxµДИЎЦµ·¶О§Ј»
ЈЁ2Ј©ЗуєЇКэyµДµјКэЈ¬АыУГµјКэЕР¶ПєЇКэµДµҐµчРФЈ¬ЗуіцєЇКэµДЧоЦµєН¶ФУ¦xµДЦµЈ®
(1)ТтОЄ![]() Ј¬ЛщТФ
Ј¬ЛщТФ![]() .
.
ФЪ![]() ЦРЈ¬
ЦРЈ¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() .
.
УЙХэПТ¶ЁАнЈ¬µГ![]() Ј¬
Ј¬
µГ![]() Ј¬
Ј¬![]() .
.
УЦФІ»Ў![]() і¤ОЄ
і¤ОЄ![]() Ј¬
Ј¬
ЛщТФ![]()
![]() .
.
(2)јЗ![]() Ј¬
Ј¬
Фт![]() Ј¬
Ј¬
Бо![]() Ј¬µГ
Ј¬µГ![]() .
.
µ±![]() ±д»ЇК±Ј¬
±д»ЇК±Ј¬![]() Ј¬
Ј¬![]() µД±д»ЇИзПВ±нЈє
µД±д»ЇИзПВ±нЈє
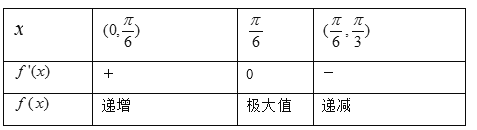
ЛщТФ![]() ФЪ
ФЪ![]() ґ¦ИЎµГј«ґуЦµЈ¬Хвёцј«ґуЦµѕНКЗЧоґуЦµЈ¬јґ
ґ¦ИЎµГј«ґуЦµЈ¬Хвёцј«ґуЦµѕНКЗЧоґуЦµЈ¬јґ![]() .
.
№Кµ±![]() К±Ј¬№гёжО»іцЧвµДЧЬКХИлЧоґуЈ¬ЧоґуЦµОЄ
К±Ј¬№гёжО»іцЧвµДЧЬКХИлЧоґуЈ¬ЧоґуЦµОЄ![]() ФЄЈ®
ФЄЈ®

 ФЖДПК¦ґуёЅРЎТ»ПЯГыК¦МбУЕЧчТµПµБРґр°ё
ФЖДПК¦ґуёЅРЎТ»ПЯГыК¦МбУЕЧчТµПµБРґр°ё іеґМ100·ЦµҐФЄУЕ»ЇБ·їјѕнПµБРґр°ё
іеґМ100·ЦµҐФЄУЕ»ЇБ·їјѕнПµБРґр°ёЎѕМвДїЎїДіЦЦЙи±ёЛжЧЕК№УГДкПЮµДФцјУЈ¬ГїДкµДО¬»¤·СПаУ¦ФцјУ![]() ПЦ¶ФТ»ЕъёГЙи±ёЅшРРµчІйЈ¬µГµЅХвЕъЙи±ёЧФ№єИлК№УГЦ®ИХЖрЈ¬З°ОеДкЖЅѕщГїМЁЙи±ёГїДкµДО¬»¤·СУГґуЦВИз±нЈє
ПЦ¶ФТ»ЕъёГЙи±ёЅшРРµчІйЈ¬µГµЅХвЕъЙи±ёЧФ№єИлК№УГЦ®ИХЖрЈ¬З°ОеДкЖЅѕщГїМЁЙи±ёГїДкµДО¬»¤·СУГґуЦВИз±нЈє
Дк·Э | 1 | 2 | 3 | 4 | 5 |
О¬»¤·С |
|
|
|
|
|
![]() ўс
ўс![]() Зуy№ШУЪtµДПЯРФ»Ш№й·ЅіМЈ»
Зуy№ШУЪtµДПЯРФ»Ш№й·ЅіМЈ»
![]() ўт
ўт![]() ИфёГЙи±ёµДјЫёсКЗГїМЁ5НтФЄЈ¬јЧИПОЄУ¦ёГК№УГВъОеДк»»Т»ґОЙи±ёЈ¬¶шТТФтИПОЄУ¦ёГК№УГВъК®Дк»»Т»ґОЙи±ёЈ¬ДгИПОЄјЧєНТТЛёьУРµААнЈїІўЛµГчАнУЙЈ®
ИфёГЙи±ёµДјЫёсКЗГїМЁ5НтФЄЈ¬јЧИПОЄУ¦ёГК№УГВъОеДк»»Т»ґОЙи±ёЈ¬¶шТТФтИПОЄУ¦ёГК№УГВъК®Дк»»Т»ґОЙи±ёЈ¬ДгИПОЄјЧєНТТЛёьУРµААнЈїІўЛµГчАнУЙЈ®
![]() ІОїј№«КЅЈє
ІОїј№«КЅЈє Ј¬
Ј¬![]()