题目内容
有以下命题:①命题“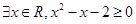 ”的否定是:“
”的否定是:“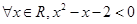 ”;
”;
②已知随机变量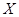 服从正态分布
服从正态分布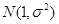 ,
,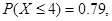 则
则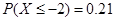 ;
;
③函数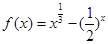 的零点在区间
的零点在区间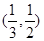 内;其中正确的命题的个数为( )
内;其中正确的命题的个数为( )
| A.0个 | B.1个 | C.2个 | D.3个 |
D
解析试题分析:存在性命题的否定是全称命题,①命题“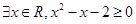 ”的否定是:“
”的否定是:“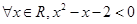 ”正确;
”正确;
因为随机变量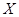 服从正态分布
服从正态分布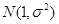 ,所以正态分布曲线对称轴为x="1," 由正态分布的性质,当
,所以正态分布曲线对称轴为x="1," 由正态分布的性质,当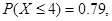 则
则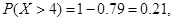 所以
所以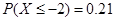 ;②正确;
;②正确;
由幂函数、指数函数的性质可知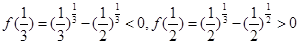 ,所以由零点存在定理,③函数
,所以由零点存在定理,③函数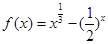 的零点在区间
的零点在区间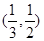 内,正确。故选D。
内,正确。故选D。
考点:本题主要考查命题的概念,全称命题与存在性命题的关系,正态分布的性质,函数零点存在定理。
点评:简单题,本题通过判断命题的真假,综合考查命题的概念,全称命题与存在性命题的关系,正态分布的性质,函数零点存在定理,对学生灵活运用数学知识解题的能力有较好的考查。

练习册系列答案
相关题目
已知命题p: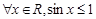 ,则
,则 为( )
为( )
A.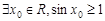 | B.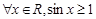 |
C.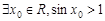 | D.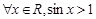 |
已知命题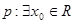 ,
,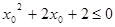 则
则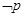 为
为
A.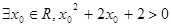 | B.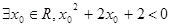 |
C.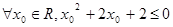 | D.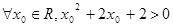 |
设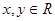 ,则“
,则“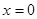 ”是“复数
”是“复数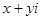 为纯虚数”的( )条件
为纯虚数”的( )条件
| A.充分而不必要 | B.必要而不充分 | C.充分必要 | D.既不充分也不必要 |
下列有关命题的说法中错误的是( )
A.命题“若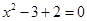 ,则 ,则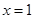 “的逆否命题为:“若 “的逆否命题为:“若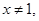 则 则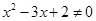 ” ” |
B.“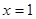 ”是“ ”是“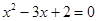 ”的充分不必要条件 ”的充分不必要条件 |
C.若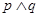 为假命题,则 为假命题,则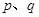 均为假命题 均为假命题 |
D.对于命题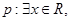 使得 使得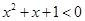 ,则 ,则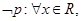 均有 均有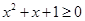 |
已知函数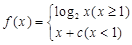 ,则“
,则“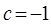 ”是“函数
”是“函数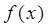 在R上
在R上
递增”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
否定结论“至多有两个解”的说法中,正确的是( )
| A.有一个解 | B.有两个解 |
| C.至少有三个解 | D.至少有两个解 |
在△ABC中“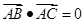 ”是“△ABC为直角三角形”的( ).
”是“△ABC为直角三角形”的( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
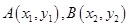 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: 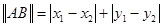 .给出下列三个命题:
.给出下列三个命题: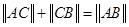 ;
;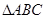 中,若∠C=90°,则
中,若∠C=90°,则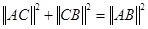 ;
;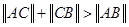 .
.