题目内容
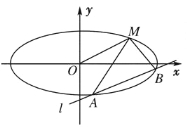
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 、
、![]() ,短轴的两个端点分别为
,短轴的两个端点分别为![]() 、
、![]() ,且
,且![]() 为等边三角形.
为等边三角形.

(1)若椭圆长轴的长为4,求椭圆![]() 的方程;
的方程;
(2)如果在椭圆![]() 上存在不同的两点
上存在不同的两点![]() 、
、![]() 关于直线
关于直线![]() 对称,求实数
对称,求实数![]() 的取值范围;
的取值范围;
(3)已知点![]() ,椭圆
,椭圆![]() 上两点
上两点![]() 、
、![]() 满足
满足![]() ,求点
,求点![]() 横坐标的取值范围.
横坐标的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
(1)根据![]() 为等边三角形,可得
为等边三角形,可得![]() ,结合椭圆长轴的长为4,即
,结合椭圆长轴的长为4,即![]() ,得
,得![]() ,从而求得椭圆的方程;
,从而求得椭圆的方程;
(2)根据等边三角形,得出a,b,c之间的关系,从而设出椭圆的方程,根据椭圆中中点弦所在直线的斜率所满足的条件,结合对称的条件,求得弦的中点坐标,保证点在椭圆内,得到相应的不等关系,得到结果;
(3)利用向量的关系,得到点的坐标之间的关系,结合隐含条件,得到相应的范围,求得结果
(1)由题意,得![]() ,
,![]() ,∴椭圆
,∴椭圆![]() 的方程为
的方程为![]() ;
;
(2)“点差法”设椭圆![]() 的方程为
的方程为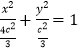 ,即
,即![]() ,
,
设![]() 、
、![]() 、
、![]() 中点
中点![]() ,
,
则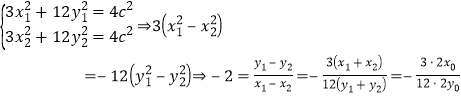 ,
,
得![]() ,又
,又![]() ,解得
,解得![]() ,
,
显然![]() 在椭圆内,∴
在椭圆内,∴![]() ,得
,得![]() ,又
,又![]() ,∴
,∴![]() ;
;
(3)设椭圆方程![]() ,即
,即![]() ,
,
方法一:(常规解法)
①过![]() 、
、![]() 的直线斜率不存在,即直线方程为
的直线斜率不存在,即直线方程为![]() 时,
时,![]() 、
、![]() ,
,
由![]() ,得
,得![]() ,
,
②过![]() 、
、![]() 的直线斜率存在,设直线方程为
的直线斜率存在,设直线方程为![]() 、
、![]() 、
、![]() ,
,
由![]() ,得
,得![]() ,
,
![]() ,
,
则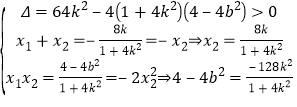 ,由
,由![]() ,可得
,可得![]() ,
,
∴![]() ,
,
综上,点![]() 横坐标的取值范围是
横坐标的取值范围是![]() .
.
方法二:设![]() ,则
,则![]() ,
,
![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴![]() ,即点
,即点![]() 横坐标的取值范围是
横坐标的取值范围是![]() .
.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目