题目内容
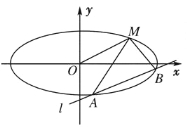
【题目】如图，已知椭圆的中心在原点，焦点在
轴上，长轴长是短轴长的2倍且经过点
，平行于
的直线
在
轴上的截距为
，直线
交椭圆于
两个不同点．
（1）求椭圆的方程；
（2）求
的取值范围．
【答案】（1）
（2）－2<m<2，且m≠0
【解析】
试题分析：（1）设出椭圆的方程，利用长轴长是短轴长的2倍且经过点M（2，1），建立方程，求出a，b，即可求椭圆的方程；（2）由直线方程代入椭圆方程，利用根的判别式，即可求m的取值范围
试题解析：（1）设椭圆方程为
（a>b>0）
则
解得
∴椭圆方程为
（2）∵直线l平行于OM，且在y轴上的截距为m
又KOM＝
，∴l的方程为：y＝
x＋m
由
∴x2＋2mx＋2m2－4＝0
∵直线l与椭圆交于A、B两个不同点，
∴Δ＝（2m）2－4（2m2－4）>0，
解得－2<m<2，且m≠0.
练习册系列答案
考前必练系列答案
相关题目
