题目内容
已知x,y,z均为正数,求证: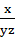 +
+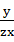 +
+ ≥
≥ +
+ +
+ .
.
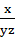 +
+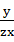 +
+ ≥
≥ +
+ +
+ .
.见解析
证明:因为x,y,z均为正数,
所以
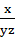 +
+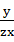 =
= ≥
≥ ,
,同理得
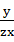 +
+ ≥
≥ ,
, +
+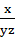 ≥
≥ (当且仅当x=y=z时,以上三式等号都成立),
(当且仅当x=y=z时,以上三式等号都成立),将上述三个不等式两边分别相加,并除以2,得
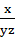 +
+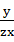 +
+ ≥
≥ +
+ +
+ .
.
练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
题目内容
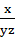 +
+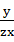 +
+ ≥
≥ +
+ +
+ .
.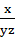 +
+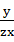 =
= ≥
≥ ,
,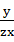 +
+ ≥
≥ ,
, +
+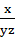 ≥
≥ (当且仅当x=y=z时,以上三式等号都成立),
(当且仅当x=y=z时,以上三式等号都成立),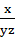 +
+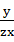 +
+ ≥
≥ +
+ +
+ .
.
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案