��Ŀ����
8������Ϊ��0��6��������˫����$\frac{{x}^{2}}{2}$-y2=1����ͬ�Ľ����ߵ�˫���߷����ǣ�������| A�� | $\frac{{x}^{2}}{12}$-$\frac{{y}^{2}}{24}$=1 | B�� | $\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1 | C�� | $\frac{{y}^{2}}{24}$-$\frac{{x}^{2}}{12}$=1 | D�� | $\frac{{x}^{2}}{24}$-$\frac{{y}^{2}}{12}$=1 |
���� �������⣬��Ҫ��˫���ߵķ���Ϊ$\frac{{x}^{2}}{2}$-y2=k����Ͻ����λ�ÿɵ�k��0���ɵ��������Ϊ��$\frac{{y}^{2}}{-k}$-$\frac{{x}^{2}}{-2k}$=1����˫���ߵļ������ʿɵ�c2=��-k��+��-2k��=36����ɵ�k��ֵ������˫���ߵı����̼��ɵô𰸣�
��� �⣺�������⣬Ҫ��˫������$\frac{{x}^{2}}{2}$-y2=1����ͬ�Ľ����ߣ��������䷽��Ϊ��$\frac{{x}^{2}}{2}$-y2=k��
�����佹��Ϊ��0��6�������佹����y������c=6������k��0��
�����������$\frac{{y}^{2}}{-k}$-$\frac{{x}^{2}}{-2k}$=1��
����c2=��-k��+��-2k��=36��
��ɵ�k=-12��
��Ҫ��˫���ߵı�����Ϊ��$\frac{{y}^{2}}{12}$-$\frac{{x}^{2}}{24}$=1��
��ѡ��B��
���� ���⿼��˫���ߵļ������ʣ��漰˫���ߵı����̣��ؼ������ս�������ͬ��˫���߷��̵��跨��

��ϰ��ϵ�д�
�����Ŀ
18����{an}�����������ĵȱ����У���a1��a2���ǡ�����{an}�ǵ������С��ģ�������
| A�� | ��Ҫ���� | B�� | ��ֶ�����Ҫ���� | ||
| C�� | ��Ҫ����������� | D�� | �Ȳ����Ҳ����Ҫ���� |
20����֪x��y����Լ������$\left\{\begin{array}{l}{x-y+1��0}\\{2x+y-a��0}\\{y-2��0}\end{array}\right.$����Ŀ�꺯��z=x-2y�����ֵ��-2����ʵ��a=��������
| A�� | -6 | B�� | -1 | C�� | 1 | D�� | 6 |
17�������ҹ����õķ�չ������Ĵ�����������������ij���������������Ҵ������������±���
��1����y����t�Ļع鷽��$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$
��2��������ع鷽��Ԥ��õ���2016�꣨t=6��������Ҵ����
�����ع鷽��$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$�У�
$\left\{\begin{array}{l}{b=\frac{\sum_{i=1}^{n}��{t}_{i}-\overline{t}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{t}_{i}-\overline{t}��^{2}}=\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}}\\{a=\overline{y}-b\overline{t}}\end{array}\right.$��
| ��� | 2011 | 2012 | 2013 | 2014 | 2015 |
| ʱ�����t | 1 | 2 | 3 | 4 | 5 |
| ������y��ǧ��Ԫ�� | 5 | 6 | 7 | 8 | 10 |
��2��������ع鷽��Ԥ��õ���2016�꣨t=6��������Ҵ����
�����ع鷽��$\widehat{y}$=$\widehat{b}$t+$\widehat{a}$�У�
$\left\{\begin{array}{l}{b=\frac{\sum_{i=1}^{n}��{t}_{i}-\overline{t}����{y}_{i}-\overline{y}��}{\sum_{i=1}^{n}��{t}_{i}-\overline{t}��^{2}}=\frac{\sum_{i=1}^{n}{t}_{i}{y}_{i}-n\overline{t}\overline{y}}{\sum_{i=1}^{n}{{t}_{i}}^{2}-n{\overline{t}}^{2}}}\\{a=\overline{y}-b\overline{t}}\end{array}\right.$��
 ��ͼ��ʾ����������ABCD-A1B1C1D1�У�AB=4��M��N�ֱ�Ϊ��A1D1��A1B1���е㣬����B��ƽ�����ƽ��AMN����ƽ����ظ����������ý�������Ϊ18��
��ͼ��ʾ����������ABCD-A1B1C1D1�У�AB=4��M��N�ֱ�Ϊ��A1D1��A1B1���е㣬����B��ƽ�����ƽ��AMN����ƽ����ظ����������ý�������Ϊ18��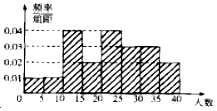 Ϊ�˸��õ���ѧ����Ӧ�߿������ľ���ijѧУ��Ը�У20���༶�����ˡ�������Ӣ���鷨��������ÿ���༶ֻ��һ��ָ����ʦ�����������˸���μӸñ�����ѧ�������������������ݣ������[0��5����[5��10����[10��15����[15��20����[20��25����[25��30����[30��35����[35��40]ʱ��������Ƶ�ʷֲ�ֱ��ͼ��ͼ��
Ϊ�˸��õ���ѧ����Ӧ�߿������ľ���ijѧУ��Ը�У20���༶�����ˡ�������Ӣ���鷨��������ÿ���༶ֻ��һ��ָ����ʦ�����������˸���μӸñ�����ѧ�������������������ݣ������[0��5����[5��10����[10��15����[15��20����[20��25����[25��30����[30��35����[35��40]ʱ��������Ƶ�ʷֲ�ֱ��ͼ��ͼ��