题目内容
若函数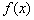 满足:集合
满足:集合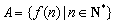 中至少存在三个不同的数构成等比数列,则称函数
中至少存在三个不同的数构成等比数列,则称函数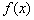 是等比源函数.
是等比源函数.
(Ⅰ)判断下列函数:①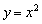 ;②
;②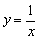 ;③
;③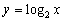 中,哪些是等比源函数?(不需证明)
中,哪些是等比源函数?(不需证明)
(Ⅱ)判断函数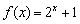 是否为等比源函数,并证明你的结论;
是否为等比源函数,并证明你的结论;
(Ⅲ)证明: ,函数
,函数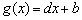 都是等比源函数.
都是等比源函数.
解:(Ⅰ)①②③都是等比源函数.
(Ⅱ)函数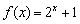 不是等比源函数.
不是等比源函数.
证明如下:
假设存在正整数 且
且 ,使得
,使得 成等比数列,
成等比数列,
 ,整理得
,整理得 ,
,
等式两边同除以 得
得 .
.
因为 ,所以等式左边为偶数,等式右边为奇数,
,所以等式左边为偶数,等式右边为奇数,
所以等式 不可能成立,
不可能成立,
所以假设不成立,说明函数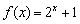 不是等比源函数.
不是等比源函数.
(Ⅲ)法1:
因为 ,都有
,都有 ,
,
所以 ,数列
,数列 都是以
都是以 为首项公差为
为首项公差为 的等差数列.
的等差数列.
 ,
, 成等比数列,
成等比数列,
因为 ,
,
 ,
,
所以
 ,
,
所以 ,函数
,函数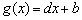 都是等比源函数.
都是等比源函数.
(Ⅲ)法2:
因为 ,都有
,都有 ,
,
所以 ,数列
,数列 都是以
都是以 为首项公差为
为首项公差为 的等差数列.
的等差数列.
由 ,(其中
,(其中 )可得
)可得
 ,整理得
,整理得
 ,
,
令 ,则
,则 ,
,
所以 ,
,
所以 ,数列
,数列 中总存在三项
中总存在三项 成等比数列.
成等比数列.
所以 ,函数
,函数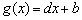 都是等比源函数.
都是等比源函数.

练习册系列答案
相关题目
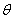 (
(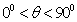 )的平面所截,截面是一个椭圆.当
)的平面所截,截面是一个椭圆.当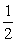 (B)
(B)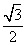 (C)
(C)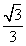 (D)
(D)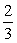
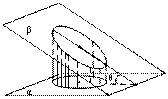
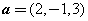 ,
,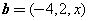 .若
.若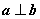 ,则
,则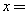 .
.  .
. 中,
中, ,求
,求 的值;
的值; 的最小正周期及其图象的所有对称轴的方程.
的最小正周期及其图象的所有对称轴的方程. 的值为
的值为 ,
,




 中,
中, ,
, 是
是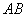 上一点,以
上一点,以 为半径的圆与
为半径的圆与 ,与
,与 切于点
切于点 ,
, ,
, ,则
,则 的长为 .
的长为 . 
 满足
满足 ,
, ,则公差
,则公差 ______;
______; ______.
______.  且
且 命题
命题 ,命题
,命题
 ,
, 是
是 的( )
的( )