题目内容
如图,在正三棱柱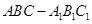 中,
中, 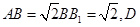 为
为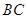 的中点。
的中点。
(Ⅰ)求证: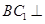 平面
平面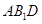 ;(Ⅱ)求直线
;(Ⅱ)求直线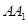 与平面
与平面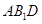 所成角的正弦值
所成角的正弦值
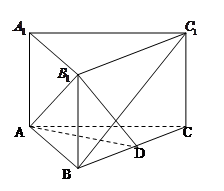
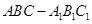 中,
中, 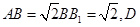 为
为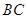 的中点。
的中点。(Ⅰ)求证:
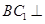 平面
平面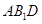 ;(Ⅱ)求直线
;(Ⅱ)求直线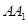 与平面
与平面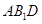 所成角的正弦值
所成角的正弦值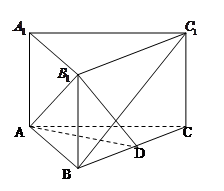
(Ⅰ)证明:以 的中点
的中点 为原点,
为原点, 分别为
分别为 轴、
轴、 轴的正方向建立空间直角坐标,则
轴的正方向建立空间直角坐标,则


∴
∴ 即
即
又∵ ∴
∴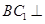 平面
平面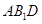 ………………………………6分
………………………………6分
(Ⅱ)解:由(Ⅰ)知, 是平面
是平面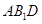 的一个法向量,
的一个法向量,
且 于是
于是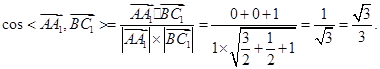
设直线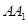 与平面
与平面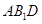 所成的角为
所成的角为 ,则
,则
故,直线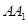 与平面
与平面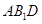 所成角的正弦值为
所成角的正弦值为
 的中点
的中点 为原点,
为原点, 分别为
分别为 轴、
轴、 轴的正方向建立空间直角坐标,则
轴的正方向建立空间直角坐标,则

∴

∴
 即
即
又∵
 ∴
∴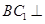 平面
平面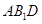 ………………………………6分
………………………………6分(Ⅱ)解:由(Ⅰ)知,
 是平面
是平面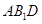 的一个法向量,
的一个法向量,且
 于是
于是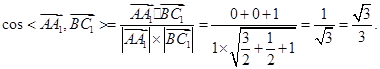
设直线
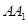 与平面
与平面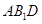 所成的角为
所成的角为 ,则
,则
故,直线
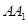 与平面
与平面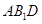 所成角的正弦值为
所成角的正弦值为
略

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
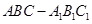 中,底面边长为
中,底面边长为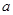 ,侧棱长为
,侧棱长为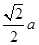 ,
,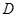 是棱
是棱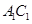 的中点.
的中点.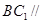 平面
平面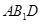 ;(Ⅱ)求二面角
;(Ⅱ)求二面角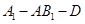 的大小;
的大小;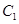 到平面
到平面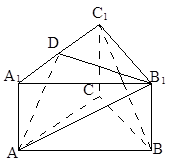
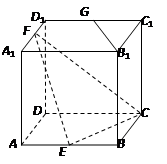
 BB1,则AB1与C1B所成角的大小为
BB1,则AB1与C1B所成角的大小为




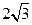 ,
,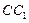 =
=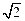 ,二面角
,二面角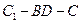 的大小为 ▲ .
的大小为 ▲ .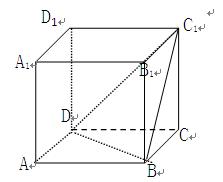
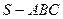 中,底面
中,底面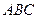 为边长等于2的等边三角形,
为边长等于2的等边三角形,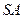 垂直于底面
垂直于底面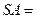
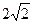 ,D为
,D为 棱柱ABC—A1B1C1中,若AB=
棱柱ABC—A1B1C1中,若AB=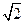 BB1,则CA1与C1B所成的角的大小是 ( )
BB1,则CA1与C1B所成的角的大小是 ( )