Question

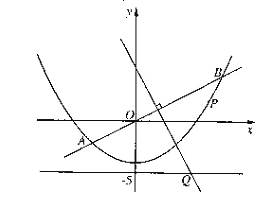
【题目】如图,抛物线E:y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心, |CO| 为半径作圆,设圆C与准线l交于不同的两点M,N.

（1）若点C的纵坐标为2,求|MN| .
（2）若|AF|2=|AM|·|AN| ,求圆C的半径.

Answer 1

【答案】
（1）

【解答】抛物线y2=4x的准线l的方程为x=-1,

由点C的纵坐标为2,得点C的坐标为(1,2),所以点C到准线l的距离d=2,又|CO|= .所以 .

（2）

【解答】设 ,则圆C的方程为 ,

即x2- x+y2-2y0y=0.由x=-1,得y2-2y0y+1+ =0,

设M(-1,y1),N(-1,y2),则:

由|AF|2=|AM|·|AN|,得|y1y2|=4,

所以 +1=4,解得y0=± ,此时Δ>0,

所以圆心C的坐标为 或 ,

从而|CO|2= ,|CO|= ,即圆C的半径为 .

【解析】垂径定理求圆的弦长MN,第 (2)问,先设C的坐标,写出圆方程,联立方程,然后结合已知条件列式求解.