题目内容
【题目】已知椭圆 C 的中心在坐标原点,焦点在 X 轴上,椭圆 C 上的点到焦点距离的最大值为3,最小值为1.
(1)求椭圆 C 的标准方程;
(2)若直线 ![]() 与椭圆 C 相交于 A,B 两点( A,B 不是左右顶点),且以 AB 为直径的图过椭圆 C 的右顶点.求证:直线 l 过定点,并求出该定点的坐标.
与椭圆 C 相交于 A,B 两点( A,B 不是左右顶点),且以 AB 为直径的图过椭圆 C 的右顶点.求证:直线 l 过定点,并求出该定点的坐标.
【答案】
(1)
【解答】由题意设椭圆的标准方程为 ![]() ,由已知得:
,由已知得: ![]() ,
,![]()
所以 椭圆的标准方程为 ![]() .
.
(2)
【解答】设 ![]() .联立
.联立 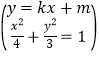
得 ![]() ,则
,则
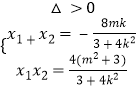
又 ![]()
因为以 AB 为直径的圆过椭圆的右顶点 ![]() ,
,
![]() ,即
,即 ![]() . 所以
. 所以![]() .
.
. .![]()
解得: ![]() ,且均满足
,且均满足 ![]() .
.
当 ![]() 时, l 的方程
时, l 的方程 ![]() ,直线过点 (2,0) ,与已知矛盾;
,直线过点 (2,0) ,与已知矛盾;
当 ![]() 时, l 的方程为
时, l 的方程为 ![]() ,直线过定点
,直线过定点 ![]() .
.
所以,直线 l 过定点,定点坐标为 ![]() .
.
【解析】(1)椭圆 ![]() 的中心在坐标原点,焦点在
的中心在坐标原点,焦点在 ![]() 轴上,椭圆
轴上,椭圆 ![]() 上的点到焦点距离的最大值为3,最小值为1;可得
上的点到焦点距离的最大值为3,最小值为1;可得 ![]() ;进而求出椭圆的标准方程.(2)中由直线交椭圆于不同两点得不等式△>0,由中点横坐标得一方程,两者联立即可求得范围,称为“方程不等式法”,解题中注意应用.
;进而求出椭圆的标准方程.(2)中由直线交椭圆于不同两点得不等式△>0,由中点横坐标得一方程,两者联立即可求得范围,称为“方程不等式法”,解题中注意应用.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
