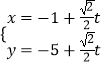题目内容
【题目】已知 ![]() =
= ![]() (
( ![]() ).
).
(Ⅰ)当 ![]() =2时,求函数
=2时,求函数 ![]() 在(1,
在(1, ![]() )处的切线方程;
)处的切线方程;
(Ⅱ)若 ![]() ≥1时,
≥1时, ![]() ≥0,求实数
≥0,求实数 ![]() 的取值范围.
的取值范围.
【答案】(Ⅰ) 当a=2时, ![]() ,所以
,所以 ![]() ,
,
∴ ![]()
∴函数 ![]() 在
在 ![]() 处的切线斜率
处的切线斜率 ![]() ,
,
∴函数 ![]() 在
在 ![]() 处的切线方程为
处的切线方程为 ![]() .
.
(Ⅱ) 若x≥1时, ![]()
∴ ![]()
设 ![]() ,
,
∴ ![]()
当 ![]() 时,
时, ![]() (当且仅当a=2,x=1时等号成立),
(当且仅当a=2,x=1时等号成立),
∴ ![]() 即
即 ![]() 在
在 ![]() 上是增函数,
上是增函数,
∴当 ![]() 时,
时, ![]() ,∴
,∴ ![]() 在
在 ![]() 上是增函数,
上是增函数,
∴当 ![]() 时,
时, ![]() ;
;
当a>2时,当 ![]() 时,
时, ![]() ,∴
,∴ ![]() 在
在 ![]() 是减函数,
是减函数,
∴当 ![]() 时,
时, ![]() ,∴
,∴ ![]() 在
在 ![]() 是减函数,
是减函数,
∴当 ![]() 时,
时, ![]() ,不满足题中条件.
,不满足题中条件.
∴实数a的取值范围为 ![]() .
.
【解析】(1)由导数算出斜率即可求出切点处方程。
(2)对g(x)进行两次求导降次,然后分情况讨论。

练习册系列答案
相关题目